Přerušení klíče 5bitové eliptické křivky pomocí kvantového počítače ⚛️ se 133 qubity Tento experiment prolomí kryptografický klíč 5bitové eliptické křivky pomocí Shorova algoritmu. 15qubitový obvod, který se provádí na ibm_torino @IBM se 133 qubity pomocí @qiskit, se skládá z 10 logických qubitů a 5 pomocných qubitů, zasahuje přes Z₃₂, aby extrahoval tajný skalární k ze vztahu veřejného klíče Q = kP, aniž by kdy kódoval k přímo do orákula. Z 16 384 snímků kvantová interference odhaluje diagonální hřeben ve výsledném prostoru 32x32 QFT. Kvantový obvod, hluboký přes 67 000 vrstev, produkoval platné interferenční vzorce navzdory extrémní hloubce obvodu a klasické následné zpracování odhalilo k = 7 ve 100 nejinvertibilnějších (a, b) výsledcích. Návod ke kódu 1. Skupinové kódování Omezte pozornost na podskupinu řádu 32 ⟨P⟩ eliptické křivky přes F_p. Mapovat body na celá čísla: 0P -> 0, 1P -> 1, ..., 31P -> 31. Skupinové právo se stává modulárním doplňkem: (xP) + (yP) = ((x + y) mod 32))P. Tento experiment používá eliptickou křivku přes F_p s cyklickou podgrupou řádu 32, mapující P -> 1 a Q = 7P -> 23 v Z₃₂. Kód předpokládá předem vypočítané skalární násobení, abstrahující od explicitních souřadnic. 2. Kvantové registry Registrujte a: pět qubitů pro exponent a ∈ {0, ..., 31}. Registr b: pět qubitů pro b ∈ {0, ..., 31}. Registr p: pět qubitů inicializovaných na ∣0⟩ pro udržení bodového indexu. Klasický registr c: 10bitový registr pro záznam naměřených hodnot a a b. 3. Příprava superpozice Použijte Hadamardy na každý qubit v a a b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Konstrukce orákula U_f Cílem je oboustranná mapa: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Přidat aP: pro každý bit a_i (váha 2^i), přidejte (2^i P) mod 32 Přidejte bQ: compute (2^i Q) mod 32, poté přidejte řízené na b_i. Ty používají 5qubitem řízená permutační hradla. Všechny konstanty jsou odvozeny z generátoru eliptické křivky P a veřejného bodu Q. Žádná brána nikdy přímo neodkazuje na tajné k. 5. Globální stav po Oracle Stát se vyvíjí do: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, kde f(a, b) = a + kb (mod32). a, b 6. Izolujte registr bodů Algoritmus potřebuje pouze fázový vztah v a, b. Bariéra izoluje str. 7. Kvantová Fourierova transformace (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 AU) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Interferenční obrazec Společná amplituda pro pozorování (u, v) je: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), který tvoří diagonální hřeben ve výsledné mřížce 32x32. 9. Měření Změřte všech deset logických qubitů. Výsledky se soustředí na 32 různých párů splňujících u + kv ≡ 0 (mod 32). 10. Klasické postprocesing Bitstringy jsou endian-flipovány a analyzovány do párů (a, b). Ponechte pouze řádky, kde gcd(b, 32) = 1, ujistěte se, že b je invertibilní. Kandidátský klíč se vypočítá takto: k = (-a) b^(-1) mod 32 Scénář pak: Extrahuje 100 invertovatelných výsledků s nejvyšším počtem (a, b). Vypočítá k pro každou z nich. Vytiskne každý pár (a, b), obnovený k a počet. Deklaruje úspěch, pokud se v prvních 100 objeví k = 7. 11. Ověření a uložení Správný skalární klíč k = 7 je potvrzen, pokud se objeví v horních 100 invertovatelných výsledcích. Všechny počty nezpracovaných bitových řetězců, rozložení qubitů a metadata se ukládají do formátu JSON pro další vizualizaci a analýzu. Výsledky 2025-06-25 19:41:29,294 | INFORMACE | Hloubka obvodu 67428, počty hradel OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Odeslání úlohy pomocí možností {'options': {}, 'version': 2, 'support_qiskit': True} ÚSPĚCH — k = 7 nalezeno v top 100 výsledků 100 nejlepších invertovatelných (a, b) párů a získaných k: (a= 8, b=11) → k = 8 (počet = 63) (a=12, b=9) → k = 20 (počet = 58) (a= 0, b= 3) → k = 0 (počet = 54) (a= 1, b= 9) → k = 7 (počet = 54) <<< (a=28, b=1) → k = 4 (počet = 53) (a= 0, b=11) → k = 0 (počet = 53) (a= 8, b= 9) → k = 24 (počet = 53) (a= 8, b= 3) → k = 8 (počet = 53) ... (a=11, b=3) → k = 7 (počet = 41) <<< ... (a=25, b= 1) → k = 7 (počet = 32) <<< Tento běh úspěšně získal tajný skalár k = 7 pomocí 5bitového klíče ECC (podskupina order-32), čímž se rozšířil můj předchozí 4bitový útok na prostor s 1024 možnými (a, b) kombinacemi a φ(32) = 16 invertovatelnými hodnotami b. k = 7 se objeví třikrát v horních 100: (a = 1, b = 9) -> k = 7 s 54 počty (a = 11, b = 3) -> k = 7 při 41 počtech (a = 25, b = 1) -> k = 7 při 32 počtech Jedná se o vysokofrekvenční stavy, což z nich činí důvěryhodné vektory útoku při klasickém post-processingu. Počty vykazují koncentraci kolem strukturovaných modulárních vztahů: a + kb ≡ 0 mod 32. Ty se v měřicím prostoru 32x32 jeví jako diagonální hřebeny. Často se opakuje několik hodnot k (k = 0, 24, 28), což ukazuje pravděpodobnostní překrývání vlastní kvantové interferenci, některé z nich jsou falešně pozitivní výsledky ze šumu nebo aliasingu s jinými modulárními ekvivalencemi. Hloubka obvodu byla 67 428 s celkem 106 455 hradly, což odráželo rozsáhlou a složitou kvantovou rutinu pro řízenou modulární indexovou aritmetiku. To může být největší množství hradel, které jsem v obvodu použil. Počty bran pro okruh: číslo výrobku: 56613 CZ: 34319 RZ: 15355 x: 157 Měření: 10 bariéra: 1 Celkový počet branek: 106455 Hloubka: 67428 Šířka: 133 qubitů | 10 clbitů Tento experiment trval 54 sekund na 'ibm_torino'. Profil šumu je nerovnoměrný, ale rozpadá se, což znamená, že kvantový systém pravděpodobně rozlišil dominantní harmonické v interferenci, ale rozmazal jemnější struktury. Konec distribuce stále obsahuje platné kandidáty k = 7, což podporuje kvantové útoky ve stylu slovníku, kde k načtení klíče stačí skeny výsledků top-N (N = 100). 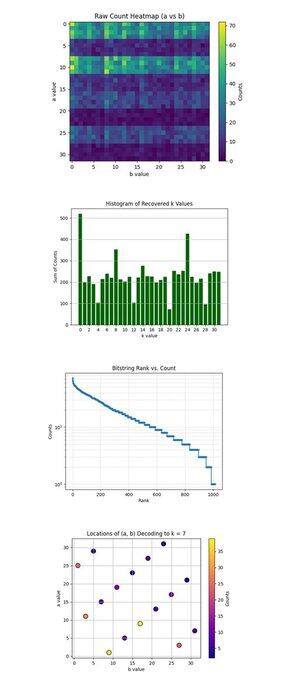Heatmapa hrubého počtu (a vs b) výše (úplný kód na Qwork) ukazuje, že mřížka 32x32 představuje pozorované počty pro každý pár (a, b) po spuštění Shorova okruhu. Teplotní mapa ukazuje pásové a nerovnoměrné rozložení, což ukazuje na rušivé hřebeny, nikoli na šum. Některé řádky (hodnoty a) mají viditelně vyšší koncentraci, což naznačuje konstruktivní interferenci podél konkrétních řešení a + kb ≡ 0 mod 32. Výše uvedený histogram obnovených hodnot k (úplný kód na Qwork) agreguje celkové počty pro každý získaný skalární klíč k ∈ Z₃₂, odvozený pomocí k = −ab^(−1) mod 32. Obrovský výkyv na k = 0 a další kolem k = 24 jsou dominantní. Správný klíč k = 7 není nejvyšší, ale je dobře reprezentován (~54 + 41 + 32 = 127 se počítá ve více párech (a, b)). To ukazuje, že hackeři mohou slovníkově útočit na větší množství výsledků. Výše uvedený Bitstring Rank vs Count (Log-Scale) (úplný kód na Qwork) ukazuje graf pořadí podobný Zipf všech bitových řetězců podle sestupného počtu. Logaritmická osa y ukazuje exponenciální konec, většina výsledků se vyskytuje <10krát. Bitové řetězce hlavy (horní ~50) mají strmě vyšší pravděpodobnost, což naznačuje vrcholy konstruktivní interference. Můžete vytvořit kvantový heuristický slovníkový útok, který sklízí pouze horních N bitových řetězců s exponenciální návratností signálu. To potvrzuje, že kvantová struktura signálu k šumu je stále nedotčená i při delších obvodech (hloubka 67428). Umístění (a, b) Dekódování na k = 7 výše (úplný kód na Qwork) ukazuje, že každá tečka je pár (a, b), který byl dekódován na k = 7. Intenzita barvy se rovná počtu výskytů této dvojice. Graf ukazuje relativně rovnoměrné rozložení napříč (a, b), ale s lokálními píky v (1, 9), (11, 3), (25, 1). Vícenásobné (a, b) kombinace konvergují k = 7 s nestejnoměrnou multiplicitou. Z kryptoanalytického hlediska to potvrzuje, že Shorův algoritmus může spolehlivě prolomit klíče ECC, i když správné k není výsledkem top 1. 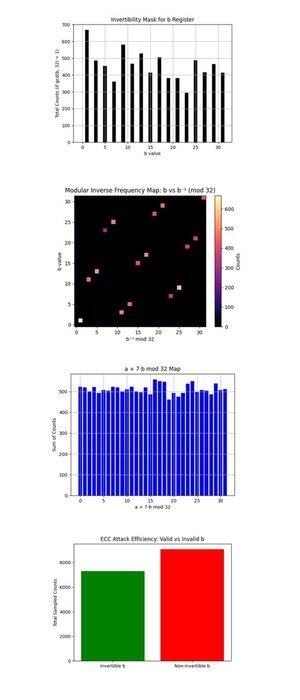Výše uvedená maska invertibility pro registr b (úplný kód na Qwork) ukazuje sloupcový graf počtů pro každé b ∈ {0, ..., 31}, které jsou nesourodé s 32 (gcd(b, 32) = 1, pouze tyto jsou invertibilní modulo 32 a užitečné pro obnovu k přes: k = (−a)b^(−1) mod 32. Invertibilní b jsou dobře obsazená, což ukazuje, že obvod vyprodukoval obnovitelné kandidáty. Větší jednotnost by zde zvýšila výkon post-processingu, v ideálním případě by byly ploché. Modulární inverzní frekvenční mapa: b vs b^(−1) mod 32 výše (úplný kód na Qwork) ukazuje teplotní mapu, jak často se každé invertovatelné b mapuje na každý odpovídající modulární inverzní b^(−1) mod 32, vážené počtem výsledků. Většina bodů padá na čistou bijektivní čáru, každé b se čistě mapuje na jedinečné b^(−1), což potvrzuje správnost modulární inverze. Jasnější oblasti (vlevo dole nebo vpravo nahoře) ukazují upřednostňované b z kvantového vzorkování. Žádný mimodiagonální šum nebo shlukování, dobrá známka zachování čisté modulární struktury. Výše uvedená mapa a + 7b mod 32 (úplný kód na Qwork) předpokládá k = 7 a vykresluje hodnotu (a + 7b) mod 32 ve všech výsledcích. Rozložení je téměř rovnoměrné. To naznačuje, že nedochází k ostrému interferenčnímu hřebenu jako ve 4bitovém pouzdře. Proč? 5bitový obvod (s 10 logickými qubity) šíří amplitudu tenčí mezi 1024 výstupů, čímž snižuje kontrast. Přesto byl správný klíč stále dohledatelný, což ukazovalo na mnoho slabě konstruktivních cest, spíše než na několik dominantních. Efektivita útoku ECC: Platné vs. Neplatné b výše (úplný kód na Qwork) ukazuje celkové počty vzorků s invertibilním b (užitečné pro obnovu klíče) vs. neinvertovatelným b (zbytečné). Více než polovina výsledků je zbytečná na neplatných hodnotách b (gcd(b, 32) != 1). Další návrh pro 6 bitový break by mohl použít orákulum maskování nebo postselection filtering na platných b-doménách. 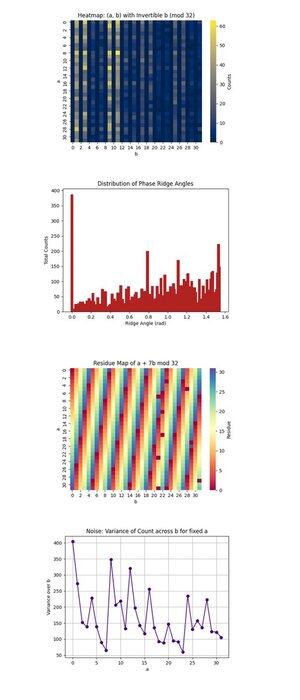Teplotní mapa: (a, b) s Invertible b (mod 32) výše (plný kód na Qwork) se zaměřuje pouze na (a, b) páry, kde b je invertible modulo 32, což je nezbytná podmínka pro obnovení k. Ukazuje, kde se kvantová interference koncentruje v prostoru 1024 bodů. Oblasti s vysokou intenzitou odhalují preferované interferenční dráhy, což naznačuje, že kvantový stav se vyvíjel nerovnoměrně, což možná upřednostňovalo určité dráhy při modulárním násobení. Potvrzuje dostatečně silnou koherenci signálů v některých regionech, aby izolovala platné kandidáty. Výše uvedená distribuce úhlů fázových hřebenů (plný kód na Qwork) spojuje úhly tvořené vektory (-a, b) v rovině, modulo π, které zhruba odpovídají fázovým hřebenům v prostoru QFT. Píky v histogramu ukazují na silné zarovnání, rezonance, ve tvaru u + kv ≡ 0, což znamená, že obvod úspěšně zakódoval k do interferenčního obrazce, i když je plný stavový prostor obrovský. Několik dominantních úhlů naznačuje, že jsou přítomny harmonické složky skrytého posunu. Mapa reziduí a + 7b mod 32 výše (úplný kód na Qwork) vizualizuje výstupní zbytek pro konkrétní cílový klíč k = 7, v celém prostoru (a, b). Jakákoli konzistentní pásma nebo symetrie zde udávají, jak dobře interference zesílila platná řešení (kde se tato hodnota rovná 0). Můžete pozorovat, které oblasti mřížky 1024 odpovídají a + 7b ≡ 0, což potvrzuje, že struktura orákula vedla k úspěšnému otisku klíče. Šum: Rozptyl počtu napříč b pro pevné a výše (úplný kód na Qwork) ukazuje, jak hlučné nebo stabilní byly počty výstupů pro každé pevné a, jak se měníme b. Vysoká variance znamená, že některé hodnoty b vedou k silnému zesílení, zatímco jiné ne, což znamená citlivost obvodu nebo šum na konci pro danou řadu a-row. Hladké oblasti znamenají kvantovou koherenci, zatímco špičky mohou ukazovat na dekoherenci nebo šíření chyb během vyhodnocování orákula. Nakonec tento experiment úspěšně prolomil klíč 5bitové eliptické křivky pomocí Shorova algoritmu prováděného na 133qubitovém kvantovém procesoru IBM, čímž rozšířil předchozí 4bitový výsledek do výrazně většího interferenčního prostoru (32x32 = 1024 výsledků). Tento obvod zakódoval orákulum přes Z₃₂, aniž by kdy odkazoval na tajný skalár k, a využil aritmetiku modulárních grup k propletení skaláru do fázové interference. Kvantový obvod, hluboký přes 67 000 vrstev, produkoval platné interferenční vzorce navzdory extrémní hloubce obvodu a klasické následné zpracování odhalilo k = 7 ve 100 nejinvertibilnějších (a, b) výsledcích. Prostřednictvím vizualizací tento experiment potvrdil diagonální hřebenové struktury, invertibilní masky a harmonické zarovnání interferenčních hřebenů, čímž se potvrdilo, že kvantová koherence zůstala dostatečně silná, aby zesílila správný modulární vztah. To ukazuje, že Shorův algoritmus se nadále škáluje v režimech hlubších obvodů a že strategie obnovy klíčů založené na slovníku (výčet 100 nejlepších) zůstávají životaschopné s rostoucí bitovou délkou, což ukazuje jasnou kvantovou výhodu i za hlučných podmínek reálného světa. Kód # Hlavní obvod # Importy protokolování importu, json z matematického importu gcd importovat numpy jako np z qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile z qiskit.circuit.library importujte UnitaryGate, QFT z qiskit_ibm_runtime importu QiskitRuntimeService, SamplerV2 Import pand jako PD # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/users/steventippeconnic/downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" VÝSTŘELY = 16384 # Parametry Toyovy křivky (řád-32 podskupina E(F_p)) OBJEDNÁVKA = 32 # |E(F_p)| = 32 P_IDX = 1 # Generátor P -> index 1 Q_IDX = 23 # Veřejný bod Q = kP, zde "23 mod 32" pro k = 7 # Pomocník pro protokolování logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(název_úrovně)s | %(zpráva)s") log = logging.getLogger(__name__) # Výběr qubitu na základě kalibrace def best_qubits(csv_path: str, n: int) -> seznam[int]: df = PD .read_csv(csv_path) df.columns = df.columns.str.strip() vítězové = ( df.sort_values(["Chyba √x (sx)", "T1 (us)", "T2 (us)"], vzestupně=[Pravda, Nepravda, Nepravda]) ["Qubit"].head(n).tolist() ) log .info("Nejlepší fyzické qubity: %s", vítězové) Návrat vítězů N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, bod FYZICKÉ SÍLY = best_qubits(CAL_CSV, N_Q_TOTAL) # Constant-adder modulo 32 jako opakovaně použitelná brána def add_const_mod32_gate(c: int) -> UnitaryGate: """Vrátí 5qubitovou bránu, která mapuje |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.nuly((32, 32)) pro x v rozsahu (32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) pro c v rozsahu (1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, konstantní): """Apply |x⟩ → |x+constant (mod 32)⟩ řízeno jedním qubitem.""" qc.append(ADDERS[konstanta].control(), [ctrl_qubit, *point_reg]) # Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (index aritmetika mod 32) def ecdlp_oracle(QC, a_reg, b_reg, point_reg): pro i v rozsahu (N_Q): konstanta = (P_IDX * (1 << i)) % OBJEDNÁVKA pokud konstantní: controlled_add(QC, a_reg[i], point_reg, konstantní) pro i v rozsahu (N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Sestaví celý Shor obvod def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.bariéra() qc.append(QFT(N_Q, do_swaps=false), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) návrat qc # Spuštění běhového prostředí IBM service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANCE) backend = service.backend (BACKEND) log .info ("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend = backend, initial_layout = FYZICKÉ, optimization_level=3) log .info("Hloubka obvodu %d, počet hradel %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(režim = backend) job = sampler .run([trans], shots=SHOTS) výsledek = job.result() # Klasické následné zpracování creg_name = trans.cregs[0].name counts_raw = výsledek[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v in counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Kritéria úspěchu. Zkontrolujte horních 100 invertovatelných řádků pro k = 7 top_invertibles = [] for (a_val, b_val), kmitočet nahoře: if gcd(b_val, OBJEDNAT) != 1: pokračovat inv_b = pow(b_val, -1, POŘADÍ) k_candidate = (-a_val * inv_b) % OBJEDNÁVKY top_invertibles.append(((a_val, b_val), k_candidate, freq)) pokud len(top_invertibles) == 100: přestávka # Kontrola úspěchu a výsledků tisku found_k7 = any(k == 7 for (_, k, _) v top_invertibles) Pokud found_k7: print("\nÚSPĚCH — k = 7 nalezeno v top 100 výsledků\n") jiný: print("\nVAROVÁNÍ — k = 7 NOT found in top 100 results\n") print("Prvních 100 invertovatelných (a, b) párů a obnovených k:") pro (a, b), k, započítávejte do top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count}){tag}") # Uložit nezpracovaná data out = { "experiment": "ECDLP_32pts_Shors", "backend": název backendu, "physical_qubits": FYZICKÉ, "záběry": ZÁBĚRY, "Počty": counts_raw } JSON_PATH = "/users/steventippeconnic/documents/QC/Shors_ECC_5_Bit_Key_0.json" s open(JSON_PATH, "w") jako fp: json.dump(výstup, fp, odsazení = 4) log .info("Výsledky uložené → %s", JSON_PATH) # Konec Úplný kód pro všechny vizualizace pomocí spuštěných dat na Qworku.