Brechen eines 5-Bit-Elliptischen-Kurven-Schlüssels mit einem 133-Qubit-Quantencomputer ⚛️ Dieses Experiment bricht einen 5-Bit elliptischen Kurven-Kryptografie-Schlüssel mithilfe von Shors Algorithmus. Ausgeführt auf @IBMs 133-Qubit ibm_torino mit @qiskit, interferiert ein 15-Qubit-Schaltkreis, der aus 10 logischen Qubits und 5 Ancilla besteht, über ℤ₃₂, um den geheimen Skalar k aus der öffentlichen Schlüsselbeziehung Q = kP zu extrahieren, ohne k jemals direkt in das Orakel zu kodieren. Aus 16.384 Schüssen zeigt die Quanteninterferenz einen diagonalen Grat im 32x32 QFT-Ergebnisraum. Der Quantenkreis, der über 67.000 Schichten tief ist, erzeugte gültige Interferenzmuster trotz extremer Schaltkreis-Tiefe, und die klassische Nachbearbeitung ergab k = 7 in den Top 100 umkehrbaren (a, b) Ergebnissen. Code-Durchlauf 1. Gruppencodierung Die Aufmerksamkeit auf die Ordnung-32-Untergruppe ⟨𝑃⟩ einer elliptischen Kurve über 𝐹_p einschränken. Punkte auf ganze Zahlen abbilden: 0𝑃 -> 0,  1𝑃 -> 1, …, 31𝑃 -> 31. Das Gruppengesetz wird zur modularen Addition: (𝑥𝑃) + (𝑦𝑃) = ((𝑥 + 𝑦) mod 32))𝑃. Dieses Experiment verwendet eine elliptische Kurve über F_p​ mit einer zyklischen Untergruppe der Ordnung 32, die P -> 1 und Q = 7P -> 23 in ℤ₃₂​ abbildet. Der Code geht von vorab berechneter skalare Multiplikation aus, die explizite Koordinaten abstrahiert. 2. Quantenregister Register a: fünf Qubits für den Exponenten 𝑎 ∈ {0, …, 31}. Register b: fünf Qubits für 𝑏 ∈ {0, …, 31}. Register p: fünf Qubits, die auf ∣0⟩ initialisiert sind, um den Punktindex zu halten. Klassisches Register c: ein 10-Bit-Register zur Aufzeichnung der gemessenen Werte von a und b. 3. Superpositionsvorbereitung Hadamards auf jedes Qubit in a und b anwenden: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Orakel-Konstruktion U_f Ziel ist eine umkehrbare Abbildung: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Füge aP hinzu: für jedes Bit a_i (Gewicht 2^𝑖), füge (2^𝑖 P) mod 32 hinzu. Füge bQ hinzu: berechne (2^𝑖 𝑄) mod 32, und füge dann kontrolliert auf 𝑏_𝑖 hinzu. Diese verwenden 5-Qubit-kontrollierte Permutationsgatter. Alle Konstanten stammen vom Generator P der elliptischen Kurve und dem öffentlichen Punkt Q. Kein Gatter verweist jemals direkt auf das geheime k. 5. Globaler Zustand nach dem Orakel Der Zustand entwickelt sich zu: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, wobei f(a, b) = a + kb (mod32). a, b 6. Isolieren des Punktregisters Der Algorithmus benötigt nur die Phasenbeziehung in 𝑎, 𝑏. Eine Barriere isoliert p. 7. Quanten-Fourier-Transformation (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Interferenzmuster Die gemeinsame Amplitude zur Beobachtung von (u, v) ist: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), was einen diagonalen Grat im 32x32 Ergebnisgitter bildet. 9. Messung Alle zehn logischen Qubits messen. Die Ergebnisse konzentrieren sich auf die 32 verschiedenen Paare, die u + kv ≡ 0 (mod 32) erfüllen. 10. Klassische Nachbearbeitung Bitstrings werden endian-flipped und in (a, b) Paare geparst. Nur Zeilen behalten, bei denen gcd⁡(b, 32) = 1, um sicherzustellen, dass b umkehrbar ist. Der Kandidatenschlüssel wird berechnet als: k = (-a) b^(-1) mod 32 Das Skript dann: Extrahiert die 100 höchsten umkehrbaren (a, b) Ergebnisse. Berechnet k für jedes. Gibt jedes (a, b) Paar, wiederhergestelltes k und Zähler aus. Erklärt den Erfolg, wenn k = 7 in den Top 100 erscheint. 11. Verifizierung und Speicherung Der korrekte Skalar k = 7 wird bestätigt, wenn er in den Top 100 umkehrbaren Ergebnissen erscheint. Alle Roh-Bitstring-Zähler, Qubit-Layouts und Metadaten werden in JSON gespeichert für weitere Visualisierungen und Analysen. Ergebnisse 2025-06-25 19:41:29,294 | INFO | Schaltkreistiefe 67428, Gatteranzahlen OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Job wird mit Optionen {'options': {}, 'version': 2, 'support_qiskit': True} eingereicht. ERFOLG — k = 7 in den Top 100 Ergebnissen gefunden Top 100 umkehrbare (a, b) Paare und wiederhergestelltes k: (a= 8, b=11) → k = 8 (Zähler = 63) (a=12, b= 9) → k = 20 (Zähler = 58) (a= 0, b= 3) → k = 0 (Zähler = 54) (a= 1, b= 9) → k = 7 (Zähler = 54) <<< (a=28, b= 1) → k = 4 (Zähler = 53) (a= 0, b=11) → k = 0 (Zähler = 53) (a= 8, b= 9) → k = 24 (Zähler = 53) (a= 8, b= 3) → k = 8 (Zähler = 53) ... (a=11, b= 3) → k = 7 (Zähler = 41) <<< ... (a=25, b= 1) → k = 7 (Zähler = 32) <<< Dieser Lauf hat erfolgreich den geheimen Skalar k = 7 mit einem 5-Bit-ECC-Schlüssel (Ordnung-32-Untergruppe) abgerufen und meine vorherige 4-Bit-Attacke auf einen Raum mit 1024 möglichen (a, b) Kombinationen und φ(32) = 16 umkehrbaren b-Werten ausgeweitet. k = 7 erscheint dreimal in den Top 100: (a = 1, b = 9) -> k = 7 mit 54 Zählern (a = 11, b = 3) -> k = 7 mit 41 Zählern (a =25, b = 1) -> k = 7 mit 32 Zählern Diese sind hochfrequente Zustände, die sie glaubwürdige Angriffsvektoren unter klassischer Nachbearbeitung machen. Die Zähler zeigen eine Konzentration um strukturierte modulare Beziehungen: a + kb ≡ 0 mod 32. Diese erscheinen als diagonale Grate im 32x32 Messraum. Mehrere k-Werte treten häufig auf (k = 0, 24, 28), was die probabilistische Überlappung zeigt, die der Quanteninterferenz innewohnt, einige davon sind falsch-positive Ergebnisse aufgrund von Rauschen oder Aliasing mit anderen modularen Äquivalenzen. Die Schaltkreistiefe betrug 67.428, mit insgesamt 106.455 Gattern, was auf eine große, komplexe Quantenroutine für kontrollierte modulare Indexarithmetik hinweist. Dies könnte die größte Anzahl von Gattern sein, die ich in einem Schaltkreis verwendet habe. Gatteranzahlen für den Schaltkreis: sx: 56613 cz: 34319 rz: 15355 x: 157 measure: 10 barrier: 1 Insgesamt Gatter: 106455 Tiefe: 67428 Breite: 133 Qubits | 10 clbits Dieses Experiment dauerte 54 Sekunden auf 'ibm_torino'. Das Rauschprofil ist nicht gleichmäßig, sondern abnehmend, was bedeutet, dass das Quantensystem wahrscheinlich dominante Harmonien in der Interferenz aufgelöst hat, aber feinere Strukturen verwischt hat. Der Verteilungsschwanz enthält immer noch gültige k = 7 Kandidaten, dies unterstützt Quantenangriffe im Wörterbuchstil, bei denen Scans der Top-N-Ergebnisse (N = 100) ausreichen, um den Schlüssel abzurufen. 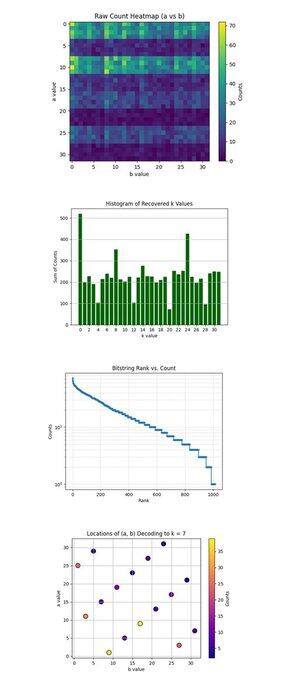Die Rohzähl-Hitzekarte (a vs b) oben (voller Code auf Qwork) zeigt ein 32x32 Gitter, das die beobachteten Zähler für jedes Paar (a, b) nach dem Ausführen von Shors Schaltkreis darstellt. Die Hitzekarte zeigt eine bandierte und ungleichmäßige Verteilung, die Interferenzgrate anzeigt, nicht Rauschen. Bestimmte Zeilen (a-Werte) haben sichtbar höhere Konzentrationen, was auf konstruktive Interferenz entlang spezifischer a + kb ≡ 0 mod 32 Lösungen hindeutet. Das Histogramm der wiederhergestellten k-Werte oben (voller Code auf Qwork) aggregiert die Gesamtzählungen für jeden wiederhergestellten skalaren Schlüssel k ∈ Z₃₂, abgeleitet über k = −ab^(−1) mod 32. Ein riesiger Anstieg bei k = 0 und ein weiterer um k = 24 sind dominant. Der korrekte Schlüssel k = 7 ist nicht der höchste, wird aber gut repräsentiert (~54 + 41 + 32 = 127 Zähler über mehrere (a, b) Paare). Dies zeigt, dass Hacker eine Wörterbuchattacke auf eine größere Anzahl von Ergebnissen durchführen können. Der Bitstring-Rang vs. Zähler (Log-Skala) oben (voller Code auf Qwork) zeigt ein Zipf-ähnliches Rangdiagramm aller Bitstrings nach absteigendem Zähler. Die Log-Skala y-Achse zeigt einen exponentiellen Schwanz, die meisten Ergebnisse treten <10 Mal auf. Der Kopf (oberste ~50) Bitstrings hat eine steil höhere Wahrscheinlichkeit, was auf konstruktive Interferenzspitzen hinweist. Man könnte einen quantenheuristischen Wörterbuchangriff aufbauen, der nur die Top-N-Bitstrings mit exponentiellem Signal-Rückfluss erntet. Dies validiert, dass die Quanten-Signal-Rausch-Struktur auch bei längeren Schaltkreisen (67428 Tiefe) intakt bleibt. Die Standorte der (a, b) Dekodierung zu k = 7 oben (voller Code auf Qwork) zeigen, dass jeder Punkt ein (a, b) Paar ist, das zu k = 7 dekodiert wurde. Die Farbintensität entspricht der Anzahl der Male, die dieses Paar aufgetreten ist. Das Diagramm zeigt eine relativ gleichmäßige Verteilung über (a, b), aber mit lokalen Spitzen bei (1, 9), (11, 3), (25, 1). Mehrere (a, b) Kombinationen konvergieren zu k = 7 mit nicht gleichmäßiger Multiplikation. Aus einer kryptanalytischen Perspektive validiert dies, dass Shors Algorithmus ECC-Schlüssel zuverlässig brechen kann, selbst wenn das korrekte k nicht das Top-1-Ergebnis ist. 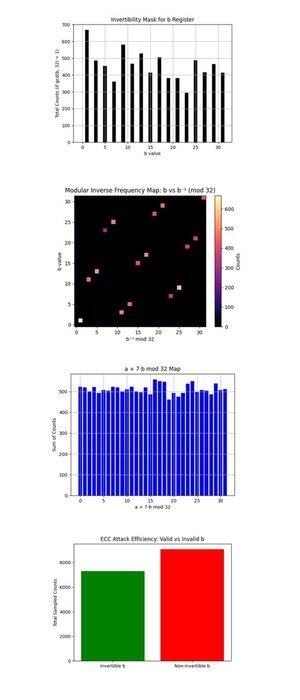Die Umkehrbarkeitsmaske für das b-Register oben (voller Code auf Qwork) zeigt ein Balkendiagramm der Zähler für jedes b ∈ {0, …, 31}, die teilerfremd zu 32 sind (gcd⁡(b, 32) = 1, nur diese sind umkehrbar modulo 32 und nützlich zur Wiederherstellung von k über: k = (−a)b^(−1) mod 32. Umkehrbare b's sind gut bevölkert, was zeigt, dass der Schaltkreis tatsächlich wiederherstellbare Kandidaten produziert hat. Mehr Gleichmäßigkeit hier würde die Nachbearbeitungskraft erhöhen, idealerweise wären diese flach. Die Frequenzkarte des modularen Inversen: b vs b^(−1) mod 32 oben (voller Code auf Qwork) zeigt eine Hitzekarte, wie oft jedes umkehrbare b auf jedes entsprechende modulare Inverse b^(−1) mod 32 abgebildet wird, gewichtet nach Ergebniszählungen. Die meisten Punkte fallen auf eine saubere bijektive Linie, jedes b wird sauber auf ein einzigartiges b^(−1) abgebildet, was die Richtigkeit der modularen Inversion bestätigt. Hellere Regionen (nahe der unteren linken oder oberen rechten Ecke) zeigen bevorzugte b's aus der quantenmäßigen Abtastung. Kein off-diagonales Rauschen oder Clustering, gutes Zeichen für eine saubere modulare Struktur, die erhalten bleibt. Die a + 7b mod 32 Karte oben (voller Code auf Qwork) geht davon aus, dass k = 7 und plottet den Wert von (a + 7b) mod 32 über alle Ergebnisse. Die Verteilung ist nahezu gleichmäßig. Dies deutet darauf hin, dass es keinen scharfen Interferenzgrat wie im 4-Bit-Fall gibt. Warum? Der 5-Bit-Schaltkreis (mit 10 logischen Qubits) verteilt die Amplitude dünner über 1024 Ergebnisse, was den Kontrast verringert. Dennoch war der korrekte Schlüssel weiterhin wiederherstellbar, was auf viele schwach konstruktive Pfade hinweist, anstatt auf einige dominante. Die ECC-Angriffseffizienz: Gültige vs. Ungültige b oben (voller Code auf Qwork) zeigt die Gesamtzählungen aus Proben mit umkehrbarem b (nützlich zur Schlüsselwiederherstellung) vs. nicht umkehrbarem b (nutzlos). Über die Hälfte der Ergebnisse sind auf ungültige b-Werte verschwendet (gcd⁡(b, 32) != 1). Das nächste Design für einen 6-Bit-Bruch könnte Orakel-Maskierung oder Nachselektion auf gültigen b-Domänen verwenden. 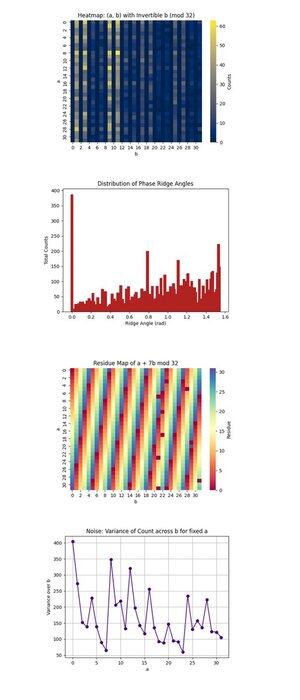Die Hitzekarte: (a, b) mit umkehrbarem b (mod 32) oben (voller Code auf Qwork) konzentriert sich nur auf (a, b) Paare, bei denen b umkehrbar modulo 32 ist, eine notwendige Bedingung zur Wiederherstellung von k. Sie zeigt, wo die Quanteninterferenz innerhalb des 1024-Punkte-Raums konzentriert ist. Die hochintensiven Regionen zeigen bevorzugte Interferenzpfade, was darauf hindeutet, dass der quantenmäßige Zustand nicht gleichmäßig evolviert ist, möglicherweise bestimmte Orbits unter modularer Multiplikation begünstigt. Es bestätigt, dass in einigen Regionen eine starke Signal-Kohärenz vorhanden ist, um gültige Kandidaten zu isolieren. Die Verteilung der Phasenrückenwinkel oben (voller Code auf Qwork) gruppiert die Winkel, die von (-a, b) Vektoren in der Ebene gebildet werden, modulo π, die grob den Phasenrücken im QFT-Raum entsprechen. Spitzen im Histogramm zeigen starke Ausrichtungen, Resonanzen, der Form u + kv ≡ 0, was bedeutet, dass der Schaltkreis erfolgreich k in das Interferenzmuster kodiert hat, obwohl der gesamte Zustandsraum riesig ist. Die mehreren dominanten Winkel deuten darauf hin, dass Harmonien des verborgenen Verschiebes vorhanden sind. Die Restkarte von a + 7b mod 32 oben (voller Code auf Qwork) visualisiert den Ausgangsrest für den spezifischen Zielschlüssel k = 7, über den gesamten (a, b) Raum. Konsistente Bänder oder Symmetrien hier zeigen, wie gut die Interferenz gültige Lösungen verstärkt hat (wo dieser Wert 0 entspricht). Man kann beobachten, welche Regionen des 1024-Gitters zu a + 7b ≡ 0 entsprechen, was validiert, dass die Struktur des Orakels zu einer erfolgreichen Schlüsselprägung geführt hat. Das Rauschen: Varianz der Zählung über b für festes a oben (voller Code auf Qwork) zeigt, wie rauschig oder stabil die Ausgangszählungen für jedes feste a waren, während wir b variieren. Hohe Varianz bedeutet, dass einige b-Werte zu starker Verstärkung führen, während andere dies nicht tun, was auf die Empfindlichkeit des Schaltkreises oder Backend-Rauschen für diese a-Zeile hinweist. Glatte Regionen implizieren Quantenkohärenz, während Spitzen auf Dekohärenz oder Fehlerausbreitung während der Orakelbewertung hinweisen können. Am Ende hat dieses Experiment erfolgreich einen 5-Bit elliptischen Kurven-Schlüssel mit Shors Algorithmus gebrochen, der auf IBMs 133-Qubit-Quantenprozessor ausgeführt wurde, und das vorherige 4-Bit-Ergebnis in einen signifikant größeren Interferenzraum (32x32 = 1024 Ergebnisse) ausgeweitet. Dieser Schaltkreis kodierte das Orakel über ℤ₃₂, ohne jemals den geheimen Skalar k zu referenzieren, und nutzte die modulare Gruppenarithmetik, um den Skalar in die Phaseninterferenz zu verflechten. Der Quantenkreis, der über 67.000 Schichten tief ist, erzeugte gültige Interferenzmuster trotz extremer Schaltkreis-Tiefe, und die klassische Nachbearbeitung ergab k = 7 in den Top 100 umkehrbaren (a, b) Ergebnissen. Durch Visualisierungen bestätigte dieses Experiment diagonale Gratstrukturen, Umkehrbarkeitsmasken und harmonische Ausrichtungen von Interferenzgraten, was validiert, dass die Quantenkohärenz stark genug blieb, um die korrekte modulare Beziehung zu verstärken. Dies stellt fest, dass Shors Algorithmus weiterhin unter tieferen Schaltkreisregimen skaliert und dass dictionary-basierte Schlüsselwiederherstellungsstrategien (Top 100 Aufzählung) weiterhin praktikabel sind, während die Bitlänge zunimmt, was einen klaren quantenmäßigen Vorteil selbst unter rauschhaften realen Bedingungen zeigt. Code # Hauptschaltkreis # Importe import logging, json from math import gcd import numpy as np from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile from qiskit.circuit.library import UnitaryGate, QFT from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 import pandas as pd # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SHOTS = 16384 # Toy-Kurvenparameter (Ordnung-32-Untergruppe von E(F_p)) ORDER = 32 # |E(F_p)| = 32 P_IDX = 1 # Generator P -> Index 1 Q_IDX = 23 # Öffentlicher Punkt Q = kP, hier „23 mod 32“ für k = 7 # Logging-Helfer logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(levelname)s | %(message)s") log = logging.getLogger(__name__) # Kalibrierungsbasierte Qubit-Auswahl def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() winners = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascending=[True, False, False]) ["Qubit"].head(n).tolist() ) log .info("Beste physische Qubits: %s", winners) return winners N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, Punkt PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL) # Konstanten-Addierer modulo 32 als wiederverwendbares Gatter def add_const_mod32_gate(c: int) -> UnitaryGate: """Gibt ein 5‑Qubit-Gatter zurück, das |x⟩ ↦ |x+c (mod 32)⟩ abbildet.""" mat = np.zeros((32, 32)) for x in range(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant): """Wendet |x⟩ → |x+Konstanten (mod 32)⟩ kontrolliert durch ein Qubit an.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Orakel U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (Indexarithmetik mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): for i in range(N_Q): constant = (P_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, a_reg[i], point_reg, constant) for i in range(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Vollständigen Shor-Schaltkreis erstellen def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) return qc # IBM Runtime-Ausführung service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANCE) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=PHYSICAL, optimization_level=3) log .info("Schaltkreistiefe %d, Gatteranzahlen %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) result = job.result() # Klassische Nachbearbeitung creg_name = trans.cregs[0].name counts_raw = result[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v in counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Erfolgskriterien. Überprüfen Sie die obersten 100 umkehrbaren Zeilen auf k = 7 top_invertibles = [] for (a_val, b_val), freq in top: if gcd(b_val, ORDER) != 1: continue inv_b = pow(b_val, -1, ORDER) k_candidate = (-a_val * inv_b) % ORDER top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: break # Überprüfen auf Erfolg und Ergebnisse ausgeben found_k7 = any(k == 7 for (_, k, _) in top_invertibles) if found_k7: print("\nERFOLG — k = 7 in den Top 100 Ergebnissen gefunden\n") else: print("\nWARNUNG — k = 7 NICHT in den Top 100 Ergebnissen gefunden\n") print("Top 100 umkehrbare (a, b) Paare und wiederhergestelltes k:") for (a, b), k, count in top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (Zähler = {count}){tag}") # Rohdaten speichern out = { "experiment": "ECDLP_32pts_Shors", "backend": backend .name, "physische_qubits": PHYSICAL, "shots": SHOTS, "counts": counts_raw } JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json" with open(JSON_PATH, "w") as fp: json.dump(out, fp, indent=4) log .info("Ergebnisse gespeichert → %s", JSON_PATH) # Ende Voller Code für alle Visualisierungen unter Verwendung von Ausführungsdaten auf Qwork.