Разбивка 5-битного ключа эллиптической кривой с помощью 133-кубитного квантового компьютера ⚛️ Этот эксперимент разбивает 5-битный криптографический ключ эллиптической кривой с использованием алгоритма Шора. Выполненный на 133-кубитном ibm_torino от @IBM с @qiskit, 15-кубитная схема, состоящая из 10 логических кубитов и 5 анциллярных, интерферирует над ℤ₃₂, чтобы извлечь секретный скаляр k из отношения открытого ключа Q = kP, не кодируя k напрямую в оракул. Из 16,384 попыток квантовая интерференция выявляет диагональный гребень в пространстве результатов QFT размером 32x32. Квантовая схема, глубиной более 67,000 слоев, произвела действительные интерференционные паттерны, несмотря на экстремальную глубину схемы, а классическая постобработка выявила k = 7 в 100 лучших обратимых (a, b) результатах. Обзор кода 1. Кодирование групп Сосредоточьте внимание на подгруппе порядка 32 ⟨𝑃⟩ эллиптической кривой над 𝐹_p. Отображение точек на целые числа: 0𝑃 -> 0,  1𝑃 -> 1, …, 31𝑃 -> 31. Групповая операция становится модульным сложением: (𝑥𝑃) + (𝑦𝑃) = ((𝑥 + 𝑦) mod 32))𝑃. Этот эксперимент использует эллиптическую кривую над F_p​ с циклической подгруппой порядка 32, отображая P -> 1 и Q = 7P -> 23 в ℤ₃₂​. Код предполагает предварительно вычисленное скалярное умножение, абстрагируя явные координаты. 2. Квантовые регистры Регистры a: пять кубитов для экспоненты 𝑎 ∈ {0, …, 31}. Регистры b: пять кубитов для 𝑏 ∈ {0, …, 31}. Регистры p: пять кубитов, инициализированных в ∣0⟩ для хранения индекса точки. Классический регистр c: 10-битный регистр для записи измеренных значений a и b. 3. Подготовка суперпозиции Примените оператор Адамара ко всем кубитам в a и b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Конструкция оракула U_f Цель - обратное отображение: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Добавьте aP: для каждого бита a_i (вес 2^𝑖), добавьте (2^𝑖 P) mod 32 Добавьте bQ: вычислите (2^𝑖 𝑄) mod 32, затем добавьте контролируемо по 𝑏_𝑖. Эти операции используют 5-кубитные контролируемые перестановочные ворота. Все константы происходят от генератора эллиптической кривой P и открытой точки Q. Ни одно ворота никогда не ссылается напрямую на секрет k. 5. Глобальное состояние после оракула Состояние эволюционирует в: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, где f(a, b) = a + kb (mod32). a, b 6. Изоляция регистра точки Алгоритму нужно только фазовое соотношение в 𝑎, 𝑏. Барьер изолирует p. 7. Квантовое преобразование Фурье (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Интерференционный паттерн Совместная амплитуда для наблюдения (u, v) равна: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), что формирует диагональный гребень в сетке результатов 32x32. 9. Измерение Измерьте все десять логических кубитов. Результаты сосредоточены на 32 различных парах, удовлетворяющих u + kv ≡ 0 (mod 32). 10. Классическая постобработка Битовые строки переворачиваются по порядку и разбиваются на пары (a, b). Оставьте только строки, где gcd⁡(b, 32) = 1, обеспечивая, что b обратимо. Кандидат на ключ вычисляется как: k = (-a) b^(-1) mod 32 Скрипт затем: Извлекает 100 лучших обратимых (a, b) результатов. Вычисляет k для каждого. Печатает каждую пару (a, b), восстановленный k и количество. Объявляет успех, если k = 7 появляется в 100 лучших. 11. Проверка и хранение Правильный скаляр k = 7 подтверждается, если он появляется в 100 лучших обратимых результатах. Все сырые подсчеты битовых строк, раскладка кубитов и метаданные сохраняются в JSON для дальнейшей визуализации и анализа. Результаты 2025-06-25 19:41:29,294 | INFO | Глубина схемы 67428, количество ворот OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Отправка задания с использованием параметров {'options': {}, 'version': 2, 'support_qiskit': True} УСПЕХ — k = 7 найден в 100 лучших результатах 100 лучших обратимых (a, b) пар и восстановленный k: (a= 8, b=11) → k = 8 (count = 63) (a=12, b= 9) → k = 20 (count = 58) (a= 0, b= 3) → k = 0 (count = 54) (a= 1, b= 9) → k = 7 (count = 54) <<< (a=28, b= 1) → k = 4 (count = 53) (a= 0, b=11) → k = 0 (count = 53) (a= 8, b= 9) → k = 24 (count = 53) (a= 8, b= 3) → k = 8 (count = 53) ... (a=11, b= 3) → k = 7 (count = 41) <<< ... (a=25, b= 1) → k = 7 (count = 32) <<< Этот запуск успешно извлек секретный скаляр k = 7, используя 5-битный ключ ECC (подгруппа порядка 32), расширяя мою предыдущую атаку на 4 бита до пространства с 1024 возможными (a, b) комбинациями и φ(32) = 16 обратимыми значениями b. k = 7 появляется трижды в 100 лучших: (a = 1, b = 9) -> k = 7 с 54 подсчетами (a = 11, b = 3) -> k = 7 с 41 подсчетом (a =25, b = 1) -> k = 7 с 32 подсчетами Это высокочастотные состояния, что делает их надежными векторами атаки при классической постобработке. Подсчеты демонстрируют концентрацию вокруг структурированных модульных отношений: a + kb ≡ 0 mod 32. Эти отношения появляются как диагональные гребни в пространстве измерений 32x32. Несколько значений k часто повторяются (k = 0, 24, 28), показывая вероятностное перекрытие, присущее квантовой интерференции, некоторые из них являются ложными положительными результатами из-за шума или алиасинга с другими модульными эквивалентностями. Глубина схемы составила 67,428, с общим количеством 106,455 ворот, что отражает большую, сложную квантовую рутину для контролируемой модульной индексной арифметики. Это может быть наибольшее количество ворот, которое я использовал в схеме. Количество ворот для схемы: sx: 56613 cz: 34319 rz: 15355 x: 157 measure: 10 barrier: 1 Всего ворот: 106455 Глубина: 67428 Ширина: 133 кубита | 10 клбит Этот эксперимент занял 54 секунды для завершения на 'ibm_torino'. Профиль шума неравномерный, но убывающий, что означает, что квантовая система, вероятно, разрешила доминирующие гармоники в интерференции, но размывала более тонкие структуры. Хвост распределения все еще содержит действительные кандидаты k = 7, это поддерживает атаки в стиле словарей, где сканирование топ-N результатов (N = 100) достаточно для извлечения ключа. 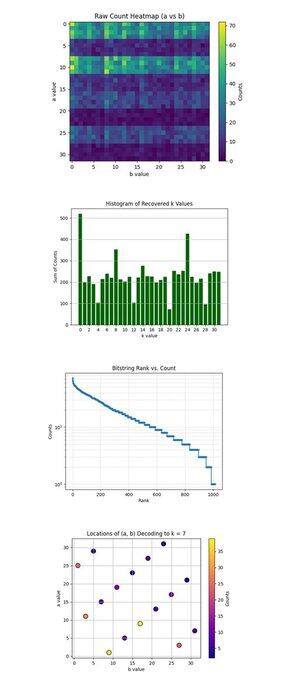Сырой тепловая карта подсчетов (a против b) выше (полный код на Qwork) показывает сетку 32x32, представляющую наблюдаемые подсчеты для каждой пары (a, b) после запуска схемы Шора. Тепловая карта показывает полосатое и неравномерное распределение, указывающее на интерференционные гребни, а не шум. Некоторые строки (значения a) имеют заметно более высокую концентрацию, что предполагает конструктивную интерференцию вдоль конкретных решений a + kb ≡ 0 mod 32. Гистограмма восстановленных значений k выше (полный код на Qwork) агрегирует общие подсчеты для каждого восстановленного скалярного ключа k ∈ Z₃₂, полученного через k = −ab^(−1) mod 32. Огромный пик при k = 0 и другой около k = 24 являются доминирующими. Правильный ключ k = 7 не является самым высоким, но хорошо представлен (~54 + 41 + 32 = 127 подсчетов по нескольким парам (a, b)). Это показывает, что хакеры могут атаковать словарем большее количество результатов. Ранг битовой строки против подсчета (логарифмическая шкала) выше (полный код на Qwork) показывает график рангов в стиле Ципфа всех битовых строк по убыванию подсчета. Логарифмическая шкала по оси y показывает экспоненциальный хвост, большинство результатов происходит <10 раз. Головка (верхние ~50) битовых строк имеет значительно более высокую вероятность, указывая на пики конструктивной интерференции. Вы могли бы построить квантовую эвристическую атаку словарем, которая собирает только верхние N битовые строки с экспоненциальной отдачей по сигналу. Это подтверждает, что структура квантового сигнала к шуму все еще сохраняется, даже с более длинными схемами (67428 глубина). Расположение (a, b) декодирования для k = 7 выше (полный код на Qwork) показывает, что каждая точка является парой (a, b), которая декодировалась в k = 7. Интенсивность цвета равна количеству раз, когда эта пара встречалась. График показывает относительно равномерное распределение по (a, b), но с локальными пиками при (1, 9), (11, 3), (25, 1). Несколько комбинаций (a, b) сходятся к k = 7 с неравномерной кратностью. С точки зрения криптоанализа это подтверждает, что алгоритм Шора может надежно разбивать ключи ECC, даже когда правильный k не является самым верхним результатом. 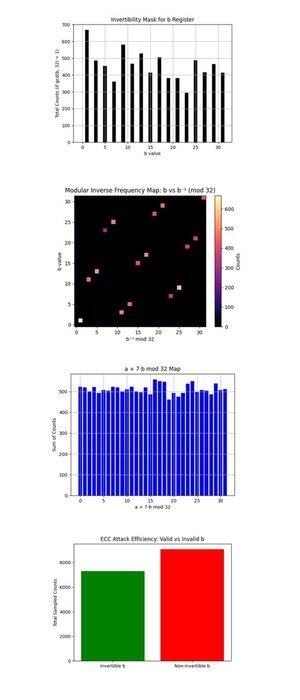Маска обратимости для регистра b выше (полный код на Qwork) показывает столбчатую диаграмму подсчетов для каждого b ∈ {0, …, 31}, которые взаимно просты с 32 (gcd⁡(b, 32) = 1, только эти обратимы по модулю 32 и полезны для восстановления k через: k = (−a)b^(−1) mod 32. Обратимые b хорошо представлены, показывая, что схема действительно произвела восстанавливаемые кандидаты. Более равномерное распределение здесь увеличило бы мощность постобработки, в идеале, они должны быть плоскими. Карта частоты модульного обратного: b против b^(−1) mod 32 выше (полный код на Qwork) показывает тепловую карту того, как часто каждый обратимый b отображается на соответствующий модульный обратный b^(−1) mod 32, взвешенный по количеству результатов. Большинство точек попадают на чистую биективную линию, каждый b отображается четко на уникальный b^(−1), подтверждая правильность модульного обращения. Более яркие области (вблизи нижнего левого или верхнего правого угла) показывают предпочтительные b из квантового выборки. Нет шумов или кластеризации вне диагонали, что является хорошим знаком сохранения чистой модульной структуры. Карта a + 7b mod 32 выше (полный код на Qwork) предполагает k = 7 и отображает значение (a + 7b) mod 32 по всем результатам. Распределение почти равномерное. Это предполагает отсутствие резкого интерференционного гребня, как в случае с 4 битами. Почему? 5-битная схема (с 10 логическими кубитами) распределяет амплитуду тоньше по 1024 результатам, уменьшая контраст. Тем не менее, правильный ключ все еще был восстанавливаем, указывая на множество слабо конструктивных путей, а не на несколько доминирующих. Эффективность атаки ECC: действительные против недействительных b выше (полный код на Qwork) показывает общее количество подсчетов из выборок с обратимыми b (полезными для восстановления ключа) против недействительных b (бесполезных). Более половины результатов потрачены на недействительные значения b (gcd⁡(b, 32) != 1). Следующий проект для разбиения на 6 бит может использовать маскировку оракула или фильтрацию поствыборки по действительным областям b. 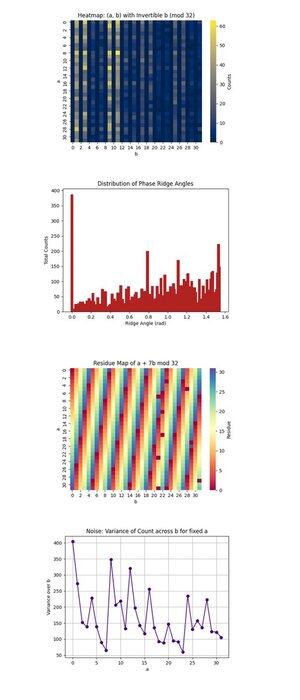Тепловая карта: (a, b) с обратимыми b (mod 32) выше (полный код на Qwork) сосредотачивается только на парах (a, b), где b обратимо по модулю 32, что является необходимым условием для восстановления k. Она показывает, где квантовая интерференция концентрируется в пространстве из 1024 точек. Области высокой интенсивности выявляют предпочтительные пути интерференции, предполагая, что квантовое состояние развивалось неравномерно, возможно, предпочитая определенные орбиты при модульном умножении. Это подтверждает достаточно сильную когерентность сигнала в некоторых областях, чтобы изолировать действительных кандидатов. Распределение углов фазового гребня выше (полный код на Qwork) группирует углы, образованные векторами (-a, b) в плоскости, по модулю π, которые примерно соответствуют фазовым гребням в пространстве QFT. Пики в гистограмме указывают на сильные выравнивания, резонансы, вида u + kv ≡ 0, что означает, что схема успешно закодировала k в интерференционном паттерне, даже несмотря на то, что полное пространство состояний велико. Множественные доминирующие углы предполагают наличие гармоник скрытого сдвига. Карта остатков a + 7b mod 32 выше (полный код на Qwork) визуализирует выходной остаток для конкретного целевого ключа k = 7, по всему пространству (a, b). Любые последовательные полосы или симметрии здесь указывают на то, насколько хорошо интерференция усилила действительные решения (где это значение равно 0). Вы можете наблюдать, какие области 1024 решетки соответствуют a + 7b ≡ 0, подтверждая, что структура оракула привела к успешной печати ключа. Шум: Дисперсия подсчета по b для фиксированного a выше (полный код на Qwork) показывает, насколько шумные или стабильные были выходные подсчеты для каждого фиксированного a при изменении b. Высокая дисперсия означает, что некоторые значения b приводят к сильному усилению, в то время как другие - нет, что подразумевает чувствительность схемы или шум на заднем плане для этой строки a. Гладкие области подразумевают квантовую когерентность, в то время как пики могут указывать на декогеренцию или распространение ошибок во время оценки оракула. В конце концов, этот эксперимент успешно разбил 5-битный ключ эллиптической кривой с использованием алгоритма Шора, выполненного на 133-кубитном квантовом процессоре IBM, расширяя предыдущий результат на 4 бита в значительно более крупное пространство интерференции (32x32 = 1024 результата). Эта схема закодировала оракул над ℤ₃₂, никогда не ссылаясь на секретный скаляр k, и использовала модульную групповую арифметику, чтобы запутать скаляр в фазовой интерференции. Квантовая схема, глубиной более 67,000 слоев, произвела действительные интерференционные паттерны, несмотря на экстремальную глубину схемы, а классическая постобработка выявила k = 7 в 100 лучших обратимых (a, b) результатах. Через визуализации этот эксперимент подтвердил диагональные структуры гребней, маски обратимости и гармоническое выравнивание интерференционных гребней, подтверждая, что квантовая когерентность оставалась достаточно сильной, чтобы усилить правильное модульное соотношение. Это устанавливает, что алгоритм Шора продолжает масштабироваться в условиях более глубоких схем и что стратегии восстановления ключей на основе словарей (перечисление 100 лучших) остаются жизнеспособными по мере увеличения длины битов, показывая явное квантовое преимущество даже в условиях реального шума. Код # Основная схема # Импорт import logging, json from math import gcd import numpy as np from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile from qiskit.circuit.library import UnitaryGate, QFT from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 import pandas as pd # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SHOTS = 16384 # Параметры игрушечной кривой (подгруппа порядка 32 E(F_p)) ORDER = 32 # |E(F_p)| = 32 P_IDX = 1 # Генератор P -> индекс 1 Q_IDX = 23 # Открытая точка Q = kP, здесь "23 mod 32" для k = 7 # Помощник для ведения журнала logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(levelname)s | %(message)s") log = logging.getLogger(__name__) # Выбор кубитов на основе калибровки def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() winners = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascending=[True, False, False]) ["Qubit"].head(n).tolist() ) log .info("Лучшие физические кубиты: %s", winners) return winners N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, точка PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL) # Константный аддер по модулю 32 как повторно используемое ворота def add_const_mod32_gate(c: int) -> UnitaryGate: """Возвращает 5-кубитное ворота, которое отображает |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) for x in range(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant): """Применить |x⟩ → |x+constant (mod 32)⟩, контролируемое одним кубитом.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Оракул U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (индексная арифметика mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): for i in range(N_Q): constant = (P_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, a_reg[i], point_reg, constant) for i in range(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Построить полную схему Шора def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) return qc # Выполнение IBM Runtime service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANCE) backend = service.backend(BACKEND) log .info("Бэкэнд → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=PHYSICAL, optimization_level=3) log .info("Глубина схемы %d, количество ворот %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) result = job.result() # Классическая постобработка creg_name = trans.cregs[0].name counts_raw = result[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v in counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Критерии успеха. Проверьте 100 лучших обратимых строк на k = 7 top_invertibles = [] for (a_val, b_val), freq in top: if gcd(b_val, ORDER) != 1: continue inv_b = pow(b_val, -1, ORDER) k_candidate = (-a_val * inv_b) % ORDER top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: break # Проверьте на успех и напечатайте результаты found_k7 = any(k == 7 for (_, k, _) in top_invertibles) if found_k7: print("\nУСПЕХ — k = 7 найден в 100 лучших результатах\n") else: print("\nПРЕДУПРЕЖДЕНИЕ — k = 7 НЕ найден в 100 лучших результатах\n") print("100 лучших обратимых (a, b) пар и восстановленный k:") for (a, b), k, count in top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count}){tag}") # Сохранить сырые данные out = { "experiment": "ECDLP_32pts_Shors", "backend": backend .name, "physical_qubits": PHYSICAL, "shots": SHOTS, "counts": counts_raw } JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json" with open(JSON_PATH, "w") as fp: json.dump(out, fp, indent=4) log .info("Результаты сохранены → %s", JSON_PATH) # Конец Полный код для всех визуализаций с использованием данных запуска на Qwork.