Rompiendo una clave de curva elíptica de 5 bits con una computadora cuántica de 133 qubits ⚛️ Este experimento rompe una clave criptográfica de curva elíptica de 5 bits utilizando el algoritmo de Shor. Ejecutado en el ibm_torino de @IBM con @qiskit, un circuito de 15 qubits, compuesto por 10 qubits lógicos y 5 ancillas, interfiere sobre ℤ₃₂ para extraer el escalar secreto k de la relación de clave pública Q = kP, sin nunca codificar k directamente en el oráculo. De 16,384 disparos, la interferencia cuántica revela una cresta diagonal en el espacio de resultados de QFT de 32x32. El circuito cuántico, con más de 67,000 capas de profundidad, produjo patrones de interferencia válidos a pesar de la extrema profundidad del circuito, y el procesamiento clásico posterior reveló k = 7 en los 100 mejores resultados invertibles (a, b). Recorrido del código 1. Codificación de grupos Restringir la atención al subgrupo de orden 32 ⟨𝑃⟩ de una curva elíptica sobre 𝐹_p. Mapear puntos a enteros: 0𝑃 -> 0,  1𝑃 -> 1, …, 31𝑃 -> 31. La ley de grupo se convierte en adición modular: (𝑥𝑃) + (𝑦𝑃) = ((𝑥 + 𝑦) mod 32))𝑃. Este experimento utiliza una curva elíptica sobre F_p​ con un subgrupo cíclico de orden 32, mapeando P -> 1 y Q = 7P -> 23 en ℤ₃₂​. El código asume multiplicación escalar precomputada, abstraiendo las coordenadas explícitas. 2. Registros cuánticos Registro a: cinco qubits para el exponente 𝑎 ∈ {0, …, 31}. Registro b: cinco qubits para 𝑏 ∈ {0, …, 31}. Registro p: cinco qubits inicializados a ∣0⟩ para mantener el índice del punto. Registro clásico c: un registro de 10 bits para registrar los valores medidos de a y b. 3. Preparación de superposición Aplicar Hadamards a cada qubit en a y b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Construcción del oráculo U_f El objetivo es un mapa reversible: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Agregar aP: para cada bit a_i (peso 2^𝑖), agregar (2^𝑖 P) mod 32 Agregar bQ: calcular (2^𝑖 𝑄) mod 32, luego agregar controlado en 𝑏_𝑖. Estos utilizan puertas de permutación controladas de 5 qubits. Todas las constantes se derivan del generador P de la curva elíptica y del punto público Q. Ninguna puerta hace referencia directa al secreto k. 5. Estado global después del oráculo El estado evoluciona a: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, donde f(a, b) = a + kb (mod32). a, b 6. Aislar el registro de puntos El algoritmo necesita solo la relación de fase en 𝑎, 𝑏. Una barrera aisla p. 7. Transformación de Fourier cuántica (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Patrón de interferencia La amplitud conjunta para observar (u, v) es: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), que forma una cresta diagonal en la cuadrícula de resultados de 32x32. 9. Medición Medir todos los diez qubits lógicos. Los resultados se concentran en los 32 pares distintos que satisfacen u + kv ≡ 0 (mod 32). 10. Procesamiento clásico posterior Las cadenas de bits se invierten y se analizan en pares (a, b). Mantener solo filas donde gcd⁡(b, 32) = 1, asegurando que b sea invertible. La clave candidata se calcula como: k = (-a) b^(-1) mod 32 El script luego: Extrae los 100 resultados invertibles (a, b) de mayor conteo. Calcula k para cada uno. Imprime cada par (a, b), k recuperado y conteo. Declara éxito si k = 7 aparece en los 100 mejores. 11. Verificación y almacenamiento El escalar correcto k = 7 se confirma si aparece en los 100 mejores resultados invertibles. Todos los conteos de cadenas de bits en bruto, la disposición de qubits y los metadatos se guardan en JSON para una visualización y análisis posteriores. Resultados 2025-06-25 19:41:29,294 | INFO | Profundidad del circuito 67428, conteos de puertas OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'medir': 10, 'barrera': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Enviando trabajo usando opciones {'options': {}, 'version': 2, 'support_qiskit': True} ÉXITO — k = 7 encontrado en los 100 mejores resultados Los 100 mejores pares invertibles (a, b) y k recuperado: (a= 8, b=11) → k = 8 (conteo = 63) (a=12, b= 9) → k = 20 (conteo = 58) (a= 0, b= 3) → k = 0 (conteo = 54) (a= 1, b= 9) → k = 7 (conteo = 54) <<< (a=28, b= 1) → k = 4 (conteo = 53) (a= 0, b=11) → k = 0 (conteo = 53) (a= 8, b= 9) → k = 24 (conteo = 53) (a= 8, b= 3) → k = 8 (conteo = 53) ... (a=11, b= 3) → k = 7 (conteo = 41) <<< ... (a=25, b= 1) → k = 7 (conteo = 32) <<< Esta ejecución recuperó con éxito el escalar secreto k = 7 utilizando una clave ECC de 5 bits (subgrupo de orden 32), extendiendo mi ataque previo de 4 bits a un espacio con 1024 combinaciones posibles (a, b) y φ(32) = 16 valores b invertibles. k = 7 aparece tres veces en los 100 mejores: (a = 1, b = 9) -> k = 7 con 54 conteos (a = 11, b = 3) -> k = 7 con 41 conteos (a =25, b = 1) -> k = 7 con 32 conteos Estos son estados de alta frecuencia, lo que los convierte en vectores de ataque creíbles bajo procesamiento clásico posterior. Los conteos exhiben concentración alrededor de relaciones modulares estructuradas: a + kb ≡ 0 mod 32. Estas aparecen como crestas diagonales en el espacio de medición de 32x32. Varios valores de k se repiten a menudo (k = 0, 24, 28), mostrando la superposición probabilística intrínseca a la interferencia cuántica, algunos de estos son falsos positivos por ruido o aliasing con otras equivalencias modulares. La profundidad del circuito fue de 67,428, con un total de 106,455 puertas, reflejando una rutina cuántica grande y compleja para la aritmética de índice modular controlada. Esta puede ser la mayor cantidad de puertas que he utilizado en un circuito. Conteos de puertas para el circuito: sx: 56613 cz: 34319 rz: 15355 x: 157 medir: 10 barrera: 1 Total de puertas: 106455 Profundidad: 67428 Ancho: 133 qubits | 10 clbits Este experimento tomó 54 segundos para completarse en 'ibm_torino'. El perfil de ruido es no uniforme pero decreciente, lo que significa que el sistema cuántico probablemente resolvió armónicos dominantes en la interferencia pero difuminó estructuras más finas. La cola de la distribución aún contiene candidatos válidos k = 7, esto apoya ataques cuánticos de estilo diccionario donde los escaneos de resultados top-N (N = 100) son suficientes para recuperar la clave. 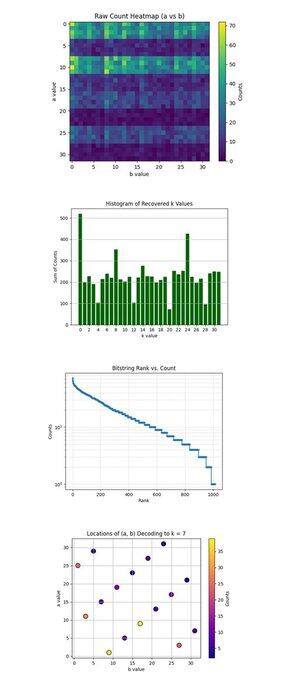El mapa de calor de conteo en bruto (a vs b) arriba (código completo en Qwork) muestra una cuadrícula de 32x32 que representa los conteos observados para cada par (a, b) después de ejecutar el circuito de Shor. El mapa de calor muestra una distribución estriada y desigual, indicando crestas de interferencia, no ruido. Ciertas filas (valores de a) tienen una concentración visiblemente más alta, sugiriendo interferencia constructiva a lo largo de soluciones específicas a + kb ≡ 0 mod 32. El histograma de valores k recuperados arriba (código completo en Qwork) agrega los conteos totales para cada clave escalar recuperada k ∈ Z₃₂, derivada a través de k = −ab^(−1) mod 32. Un gran pico en k = 0 y otro alrededor de k = 24 son dominantes. La clave correcta k = 7 no es la más alta, pero está bien representada (~54 + 41 + 32 = 127 conteos a través de múltiples pares (a, b)). Esto muestra que los hackers pueden atacar un mayor número de resultados mediante diccionario. El rango de cadenas de bits vs conteo (escala logarítmica) arriba (código completo en Qwork) muestra un gráfico de rango tipo Zipf de todas las cadenas de bits por conteo descendente. El eje y en escala logarítmica muestra una cola exponencial, la mayoría de los resultados ocurren <10 veces. La cabeza (los ~50 mejores) cadenas de bits tienen una probabilidad mucho más alta, indicando picos de interferencia constructiva. Podrías construir un ataque cuántico heurístico de diccionario que coseche solo las cadenas de bits superiores N con un retorno exponencial en la señal. Esto valida que la estructura de señal a ruido cuántica sigue intacta incluso con circuitos más largos (67428 de profundidad). Las ubicaciones de (a, b) decodificando a k = 7 arriba (código completo en Qwork) muestran que cada punto es un par (a, b) que se decodificó a k = 7. La intensidad del color equivale al número de veces que ocurrió este par. El gráfico muestra una distribución relativamente uniforme a través de (a, b), pero con picos locales en (1, 9), (11, 3), (25, 1). Múltiples combinaciones (a, b) convergen a k = 7 con multiplicidad no uniforme. Desde un punto de vista criptanalítico, esto valida que el algoritmo de Shor puede romper de manera confiable claves ECC incluso cuando el k correcto no es el resultado número 1. 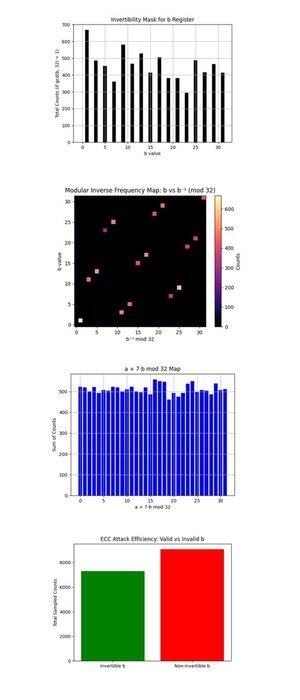La máscara de invertibilidad para el registro b arriba (código completo en Qwork) muestra un gráfico de barras de conteos para cada b ∈ {0, …, 31} que son coprimos con 32 (gcd⁡(b, 32) = 1, solo estos son invertibles módulo 32 y útiles para recuperar k a través de: k = (−a)b^(−1) mod 32. Los b invertibles están bien poblados, mostrando que el circuito produjo candidatos recuperables. Más uniformidad aquí aumentaría el poder de procesamiento posterior, idealmente, estos serían planos. El mapa de frecuencia de inversos modulares: b vs b^(−1) mod 32 arriba (código completo en Qwork) muestra un mapa de calor de cuán a menudo cada b invertible se mapea a su correspondiente inverso modular b^(−1) mod 32, ponderado por los conteos de resultados. La mayoría de los puntos caen en una línea bijectiva limpia, cada b se mapea limpiamente a un único b^(−1), confirmando la corrección de la inversión modular. Las regiones más brillantes (cerca de la esquina inferior izquierda o superior derecha) muestran b favorecidos por el muestreo cuántico. Sin ruido o agrupamiento fuera de la diagonal, buen signo de una estructura modular limpia preservada. El mapa de a + 7b mod 32 arriba (código completo en Qwork) asume k = 7 y traza el valor de (a + 7b) mod 32 a través de todos los resultados. La distribución es casi uniforme. Esto sugiere que no hay una cresta de interferencia aguda como en el caso de 4 bits. ¿Por qué? El circuito de 5 bits (con 10 qubits lógicos) dispersa la amplitud más delgada a través de 1024 resultados, reduciendo el contraste. Sin embargo, la clave correcta aún fue recuperable, indicando muchos caminos débilmente constructivos, en lugar de unos pocos dominantes. La eficiencia del ataque ECC: b válidos vs inválidos arriba (código completo en Qwork) muestra conteos totales de muestras con b invertibles (útiles para la recuperación de claves) vs. b no invertibles (inútiles). Más de la mitad de los resultados se desperdician en valores b inválidos (gcd⁡(b, 32) != 1). El próximo diseño para un rompimiento de 6 bits podría usar enmascaramiento de oráculos o filtrado de postselección en dominios b válidos. 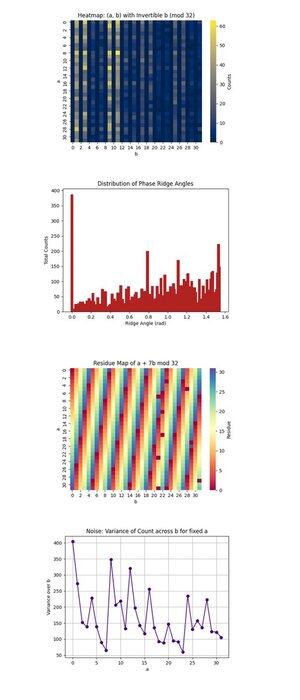El mapa de calor: (a, b) con b invertible (mod 32) arriba (código completo en Qwork) se centra solo en pares (a, b) donde b es invertible módulo 32, una condición necesaria para recuperar k. Muestra dónde la interferencia cuántica se concentra dentro del espacio de 1024 puntos. Las regiones de alta intensidad revelan caminos de interferencia preferidos, sugiriendo que el estado cuántico evolucionó de manera no uniforme, posiblemente favoreciendo ciertas órbitas bajo multiplicación modular. Confirma que hay suficiente coherencia de señal en algunas regiones para aislar candidatos válidos. La distribución de ángulos de cresta de fase arriba (código completo en Qwork) agrupa los ángulos formados por vectores (-a, b) en el plano, módulo π, que corresponden aproximadamente a crestas de fase en el espacio QFT. Picos en el histograma indican fuertes alineaciones, resonancias, de la forma u + kv ≡ 0, lo que significa que el circuito codificó con éxito k en el patrón de interferencia a pesar de que el espacio de estado completo es vasto. Los múltiples ángulos dominantes sugieren que están presentes armónicos del desplazamiento oculto. El mapa de residuos de a + 7b mod 32 arriba (código completo en Qwork) visualiza el residuo de salida para la clave objetivo específica k = 7, a través de todo el espacio (a, b). Cualquier banda o simetría consistente aquí indica cuán bien la interferencia amplificó soluciones válidas (donde este valor es igual a 0). Puedes observar qué regiones de la cuadrícula de 1024 corresponden a a + 7b ≡ 0, validando que la estructura del oráculo llevó a una exitosa impresión de clave. El ruido: varianza de conteo a través de b para a fijo arriba (código completo en Qwork) muestra cuán ruidosos o estables fueron los conteos de salida para cada a fijo a medida que variamos b. Alta varianza significa que algunos valores b conducen a una fuerte amplificación mientras que otros no, implicando sensibilidad del circuito o ruido de fondo para esa fila a. Regiones suaves implican coherencia cuántica, mientras que picos pueden señalar decoherencia o propagación de errores durante la evaluación del oráculo. Al final, este experimento rompió con éxito una clave de curva elíptica de 5 bits utilizando el algoritmo de Shor ejecutado en el procesador cuántico de 133 qubits de IBM, extendiendo el resultado previo de 4 bits a un espacio de interferencia significativamente más grande (32x32 = 1024 resultados). Este circuito codificó el oráculo sobre ℤ₃₂ sin nunca hacer referencia al escalar secreto k, y aprovechó la aritmética de grupos modulares para entrelazar el escalar en la interferencia de fase. El circuito cuántico, con más de 67,000 capas de profundidad, produjo patrones de interferencia válidos a pesar de la extrema profundidad del circuito, y el procesamiento clásico posterior reveló k = 7 en los 100 mejores resultados invertibles (a, b). A través de visualizaciones, este experimento confirmó estructuras de cresta diagonal, máscaras de invertibilidad y alineación armónica de crestas de interferencia, validando que la coherencia cuántica se mantuvo lo suficientemente fuerte como para amplificar la relación modular correcta. Esto establece que el algoritmo de Shor continúa escalando bajo regímenes de circuito más profundos y que las estrategias de recuperación de claves basadas en diccionario (enumeración de los 100 mejores) siguen siendo viables a medida que aumenta la longitud de bits, mostrando una clara ventaja cuántica incluso en condiciones ruidosas del mundo real. Código # Circuito principal # Importaciones import logging, json from math import gcd import numpy as np from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile from qiskit.circuit.library import UnitaryGate, QFT from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 import pandas as pd # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SHOTS = 16384 # Parámetros de curva de juguete (subgrupo de orden 32 de E(F_p)) ORDER = 32 # |E(F_p)| = 32 P_IDX = 1 # Generador P -> índice 1 Q_IDX = 23 # Punto público Q = kP, aquí “23 mod 32” para k = 7 # Ayudante de registro logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(levelname)s | %(message)s") log = logging.getLogger(__name__) # Selección de qubit basada en calibración def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() winners = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascending=[True, False, False]) ["Qubit"].head(n).tolist() ) log .info("Mejores qubits físicos: %s", winners) return winners N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, punto PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL) # Suma constante módulo 32 como una puerta reutilizable def add_const_mod32_gate(c: int) -> UnitaryGate: """Devuelve una puerta de 5 qubits que mapea |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) for x in range(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant): """Aplica |x⟩ → |x+constant (mod 32)⟩ controlado por un qubit.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Oráculo U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (aritmética de índice mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): for i in range(N_Q): constant = (P_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, a_reg[i], point_reg, constant) for i in range(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Construir el circuito completo de Shor def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) return qc # Ejecución de IBM Runtime service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANCE) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=PHYSICAL, optimization_level=3) log .info("Profundidad del circuito %d, conteos de puertas %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) result = job.result() # Procesamiento clásico posterior creg_name = trans.cregs[0].name counts_raw = result[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v in counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Criterios de éxito. Verificar las 100 mejores filas invertibles para k = 7 top_invertibles = [] for (a_val, b_val), freq in top: if gcd(b_val, ORDER) != 1: continue inv_b = pow(b_val, -1, ORDER) k_candidate = (-a_val * inv_b) % ORDER top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: break # Verificar el éxito e imprimir resultados found_k7 = any(k == 7 for (_, k, _) in top_invertibles) if found_k7: print("\nÉXITO — k = 7 encontrado en los 100 mejores resultados\n") else: print("\nADVERTENCIA — k = 7 NO encontrado en los 100 mejores resultados\n") print("Los 100 mejores pares invertibles (a, b) y k recuperado:") for (a, b), k, count in top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (conteo = {count}){tag}") # Guardar datos en bruto out = { "experimento": "ECDLP_32pts_Shors", "backend": backend .name, "qubits_físicos": PHYSICAL, "disparos": SHOTS, "conteos": counts_raw } JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json" with open(JSON_PATH, "w") as fp: json.dump(out, fp, indent=4) log .info("Resultados guardados → %s", JSON_PATH) # Fin Código completo para todas las visualizaciones utilizando datos de ejecución en Qwork.