Phá một Khóa Đường Cong Elliptic 5-Bit bằng Máy Tính Lượng 133-Qubit ⚛️ Thí nghiệm này phá một khóa mật mã đường cong elliptic 5-bit bằng cách sử dụng thuật toán Shor. Được thực hiện trên máy tính lượng tử 133-qubit ibm_torino của @IBM với @qiskit, một mạch 15-qubit, bao gồm 10 qubit logic và 5 ancilla, can thiệp qua ℤ₃₂ để trích xuất số vô hướng bí mật k từ mối quan hệ khóa công khai Q = kP, mà không bao giờ mã hóa k trực tiếp vào oracle. Từ 16,384 lần thử, sự can thiệp lượng tử tiết lộ một rãnh chéo trong không gian kết quả QFT 32x32. Mạch lượng tử, sâu 67,000 lớp, đã tạo ra các mẫu can thiệp hợp lệ mặc dù độ sâu mạch cực kỳ lớn, và xử lý hậu kỳ cổ điển đã tiết lộ k = 7 trong 100 kết quả có thể đảo ngược (a, b) hàng đầu. Hướng dẫn Mã 1. Mã hóa Nhóm Hạn chế sự chú ý vào nhóm con bậc 32 ⟨𝑃⟩ của một đường cong elliptic trên 𝐹_p. Ánh xạ các điểm thành số nguyên: 0𝑃 -> 0,  1𝑃 -> 1, …, 31𝑃 -> 31. Luật nhóm trở thành phép cộng theo mô-đun: (𝑥𝑃) + (𝑦𝑃) = ((𝑥 + 𝑦) mod 32))𝑃. Thí nghiệm này sử dụng một đường cong elliptic trên F_p​ với một nhóm con tuần hoàn bậc 32, ánh xạ P -> 1 và Q = 7P -> 23 trong ℤ₃₂​. Mã giả định phép nhân vô hướng đã được tính toán trước, trừu tượng hóa các tọa độ rõ ràng. 2. Đăng ký Lượng Tử Đăng ký a: năm qubit cho số mũ 𝑎 ∈ {0, …, 31}. Đăng ký b: năm qubit cho 𝑏 ∈ {0, …, 31}. Đăng ký p: năm qubit khởi tạo thành ∣0⟩ để giữ chỉ số điểm. Đăng ký cổ điển c: một đăng ký 10-bit để ghi lại các giá trị đo được của a và b. 3. Chuẩn bị Siêu Vị Trí Áp dụng Hadamards cho mỗi qubit trong a và b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Xây dựng Oracle U_f Mục tiêu là một ánh xạ đảo ngược: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Thêm aP: cho mỗi bit a_i (trọng số 2^𝑖), thêm (2^𝑖 P) mod 32 Thêm bQ: tính (2^𝑖 𝑄) mod 32, sau đó thêm điều khiển trên 𝑏_𝑖. Những điều này sử dụng các cổng hoán vị điều khiển 5-qubit. Tất cả các hằng số đều được lấy từ sinh viên của đường cong elliptic P và điểm công khai Q. Không có cổng nào tham chiếu trực tiếp đến số bí mật k. 5. Trạng Thái Toàn Cầu sau Oracle Trạng thái phát triển thành: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, trong đó f(a, b) = a + kb (mod32). a, b 6. Tách Biểu Đồ Điểm Thuật toán chỉ cần mối quan hệ pha trong 𝑎, 𝑏. Một rào cản tách biệt p. 7. Biến Đổi Fourier Lượng Tử (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Mẫu Can Thiệp Biến thể chung để quan sát (u, v) là: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), tạo thành một rãnh chéo trong lưới kết quả 32x32. 9. Đo Lường Đo tất cả mười qubit logic. Kết quả tập trung vào 32 cặp khác biệt thỏa mãn u + kv ≡ 0 (mod 32). 10. Xử Lý Hậu Cổ Điển Chuỗi bit được đảo ngược endian và phân tích thành các cặp (a, b). Chỉ giữ lại các hàng mà gcd⁡(b, 32) = 1, đảm bảo b có thể đảo ngược. Khóa ứng viên được tính toán như sau: k = (-a) b^(-1) mod 32 Kịch bản sau đó: Trích xuất 100 kết quả có thể đảo ngược (a, b) có số lượng cao nhất. Tính toán k cho mỗi. In mỗi cặp (a, b), k đã phục hồi và số lượng. Tuyên bố thành công nếu k = 7 xuất hiện trong 100 hàng đầu. 11. Xác Minh và Lưu Trữ Số vô hướng chính xác k = 7 được xác nhận nếu nó xuất hiện trong 100 kết quả có thể đảo ngược hàng đầu. Tất cả các số đếm chuỗi bit thô, bố trí qubit và siêu dữ liệu được lưu vào JSON để phân tích và hình dung thêm. Kết quả 2025-06-25 19:41:29,294 | INFO | Độ sâu mạch 67428, số lượng cổng OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Gửi công việc sử dụng tùy chọn {'options': {}, 'version': 2, 'support_qiskit': True} THÀNH CÔNG — k = 7 được tìm thấy trong 100 kết quả hàng đầu 100 cặp có thể đảo ngược (a, b) hàng đầu và k đã phục hồi: (a= 8, b=11) → k = 8 (số lượng = 63) (a=12, b= 9) → k = 20 (số lượng = 58) (a= 0, b= 3) → k = 0 (số lượng = 54) (a= 1, b= 9) → k = 7 (số lượng = 54) <<< (a=28, b= 1) → k = 4 (số lượng = 53) (a= 0, b=11) → k = 0 (số lượng = 53) (a= 8, b= 9) → k = 24 (số lượng = 53) (a= 8, b= 3) → k = 8 (số lượng = 53) ... (a=11, b= 3) → k = 7 (số lượng = 41) <<< ... (a=25, b= 1) → k = 7 (số lượng = 32) <<< Chạy này đã thành công trong việc lấy lại số vô hướng bí mật k = 7 bằng cách sử dụng khóa ECC 5-bit (nhóm con bậc 32), mở rộng cuộc tấn công 4-bit trước đó của tôi sang một không gian với 1024 kết hợp (a, b) có thể và φ(32) = 16 giá trị b có thể đảo ngược. k = 7 xuất hiện ba lần trong 100 hàng đầu: (a = 1, b = 9) -> k = 7 với 54 số lượng (a = 11, b = 3) -> k = 7 với 41 số lượng (a =25, b = 1) -> k = 7 với 32 số lượng Đây là các trạng thái tần suất cao, khiến chúng trở thành các vector tấn công đáng tin cậy dưới xử lý hậu kỳ cổ điển. Các số lượng thể hiện sự tập trung xung quanh các mối quan hệ mô-đun có cấu trúc: a + kb ≡ 0 mod 32. Những điều này xuất hiện như các rãnh chéo trong không gian đo lường 32x32. Một số giá trị k lặp lại thường xuyên (k = 0, 24, 28), cho thấy sự chồng chéo xác suất nội tại của sự can thiệp lượng tử, một số trong số này là các dương tính giả từ tiếng ồn hoặc sự đồng nhất với các tương đương mô-đun khác. Độ sâu mạch là 67,428, với tổng số 106,455 cổng, phản ánh một quy trình lượng tử lớn và phức tạp cho phép số chỉ mục mô-đun có kiểm soát. Đây có thể là số lượng cổng lớn nhất mà tôi đã sử dụng trong một mạch. Số lượng cổng cho mạch: sx: 56613 cz: 34319 rz: 15355 x: 157 measure: 10 barrier: 1 Tổng số cổng: 106455 Độ sâu: 67428 Chiều rộng: 133 qubits | 10 clbits Thí nghiệm này mất 54 giây để hoàn thành trên 'ibm_torino'. Hồ sơ tiếng ồn không đồng nhất nhưng giảm dần, có nghĩa là hệ thống lượng tử có khả năng giải quyết các hài chính trong sự can thiệp nhưng làm mờ các cấu trúc tinh vi hơn. Đuôi phân phối vẫn chứa các ứng viên k = 7 hợp lệ, điều này hỗ trợ các cuộc tấn công lượng tử kiểu từ điển nơi quét kết quả hàng đầu-N (N = 100) là đủ để lấy lại khóa. 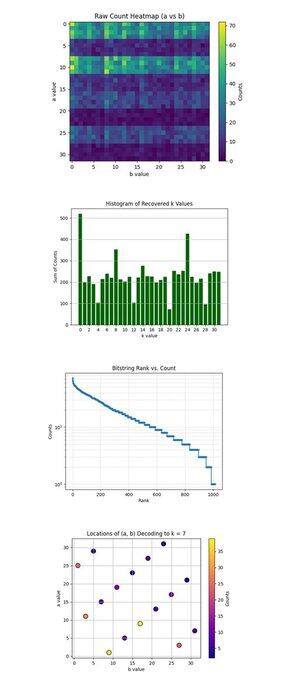Bản đồ Nhiệt Đếm Thô (a so với b) ở trên (mã đầy đủ trên Qwork) cho thấy một lưới 32x32 đại diện cho các số đếm quan sát cho mỗi cặp (a, b) sau khi chạy mạch của Shor. Bản đồ nhiệt cho thấy một phân phối băng và không đồng đều, cho thấy các rãnh can thiệp, không phải tiếng ồn. Một số hàng (giá trị a) có sự tập trung rõ rệt hơn, cho thấy sự can thiệp xây dựng dọc theo các giải pháp cụ thể a + kb ≡ 0 mod 32. Biểu đồ Tần suất Giá trị k Đã Phục Hồi ở trên (mã đầy đủ trên Qwork) tổng hợp tổng số đếm cho mỗi khóa vô hướng k ∈ Z₃₂, được lấy từ k = −ab^(−1) mod 32. Một đỉnh lớn ở k = 0 và một đỉnh khác xung quanh k = 24 là nổi bật. Khóa chính xác k = 7 không phải là cao nhất, nhưng được đại diện tốt (~54 + 41 + 32 = 127 số lượng trên nhiều cặp (a, b)). Điều này cho thấy rằng các hacker có thể tấn công từ điển một số lượng lớn kết quả. Biểu đồ Xếp hạng Chuỗi Bit so với Số lượng (Log-Scale) ở trên (mã đầy đủ trên Qwork) cho thấy một biểu đồ xếp hạng giống như Zipf của tất cả các chuỗi bit theo số lượng giảm dần. Trục y theo log cho thấy một đuôi hàm mũ, hầu hết các kết quả xảy ra <10 lần. Đầu (khoảng ~50) chuỗi bit có xác suất cao hơn nhiều, cho thấy các đỉnh can thiệp xây dựng. Bạn có thể xây dựng một cuộc tấn công từ điển lượng tử mà chỉ thu hoạch các chuỗi bit hàng đầu N với tín hiệu trả về hàm mũ. Điều này xác nhận rằng cấu trúc tín hiệu-đến-tiếng ồn lượng tử vẫn còn nguyên vẹn ngay cả với các mạch dài hơn (67428 độ sâu). Vị trí của (a, b) Giải Mã thành k = 7 ở trên (mã đầy đủ trên Qwork) cho thấy mỗi điểm là một cặp (a, b) đã giải mã thành k = 7. Cường độ màu tương đương với số lần cặp này xuất hiện. Biểu đồ cho thấy một phân phối tương đối đồng nhất trên (a, b), nhưng với các đỉnh cục bộ tại (1, 9), (11, 3), (25, 1). Nhiều kết hợp (a, b) hội tụ về k = 7 với độ đa dạng không đồng nhất. Từ quan điểm phân tích mật mã, điều này xác nhận rằng thuật toán Shor có thể phá vỡ các khóa ECC một cách đáng tin cậy ngay cả khi k chính xác không phải là kết quả hàng đầu. 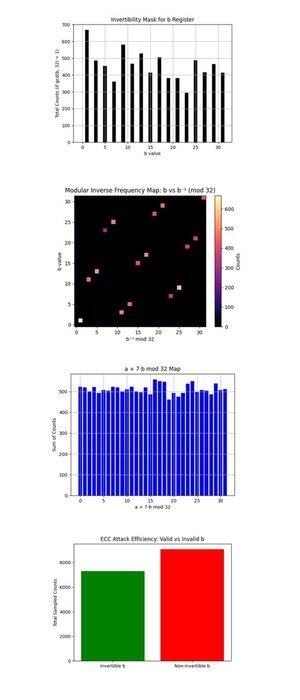Mặt nạ Đảo ngược cho Đăng ký b ở trên (mã đầy đủ trên Qwork) cho thấy một biểu đồ cột của số đếm cho mỗi b ∈ {0, …, 31} mà là nguyên tố cùng nhau với 32 (gcd⁡(b, 32) = 1, chỉ những điều này là có thể đảo ngược theo mô-đun 32 và hữu ích cho việc phục hồi k qua: k = (−a)b^(−1) mod 32. Các b có thể đảo ngược được phân bố tốt, cho thấy mạch đã tạo ra các ứng viên có thể phục hồi. Sự đồng nhất hơn ở đây sẽ tăng cường sức mạnh xử lý hậu kỳ, lý tưởng là chúng sẽ phẳng. Bản đồ Tần suất Đảo ngược: b so với b^(−1) mod 32 ở trên (mã đầy đủ trên Qwork) cho thấy một bản đồ nhiệt về tần suất mỗi b có thể đảo ngược ánh xạ đến mỗi b^(−1) tương ứng theo mô-đun 32, được trọng số theo số lượng kết quả. Hầu hết các điểm rơi vào một đường bijective sạch, mỗi b ánh xạ sạch đến một b^(−1) duy nhất, xác nhận tính chính xác của phép đảo ngược mô-đun. Các vùng sáng hơn (gần góc dưới bên trái hoặc góc trên bên phải) cho thấy các b được ưa chuộng từ việc lấy mẫu lượng tử. Không có tiếng ồn hoặc cụm ngoài đường chéo, dấu hiệu tốt của cấu trúc mô-đun sạch được bảo tồn. Bản đồ a + 7b mod 32 ở trên (mã đầy đủ trên Qwork) giả định k = 7 và vẽ giá trị của (a + 7b) mod 32 trên tất cả các kết quả. Phân phối gần như đồng nhất. Điều này gợi ý không có rãnh can thiệp sắc nét như trong trường hợp 4-bit. Tại sao? Mạch 5-bit (với 10 qubit logic) phân tán biên độ mỏng hơn trên 1024 kết quả, giảm độ tương phản. Tuy nhiên, khóa chính xác vẫn có thể phục hồi, cho thấy nhiều con đường xây dựng yếu, thay vì một vài con đường thống trị. Hiệu suất Tấn công ECC: b có thể đảo ngược so với b không thể đảo ngược ở trên (mã đầy đủ trên Qwork) cho thấy tổng số đếm từ các mẫu với b có thể đảo ngược (hữu ích cho việc phục hồi khóa) so với b không thể đảo ngược (vô dụng). Hơn một nửa số kết quả bị lãng phí vào các giá trị b không hợp lệ (gcd⁡(b, 32) != 1). Thiết kế tiếp theo cho một cuộc tấn công 6 bit có thể sử dụng che giấu oracle hoặc lọc hậu kỳ trên các miền b hợp lệ. 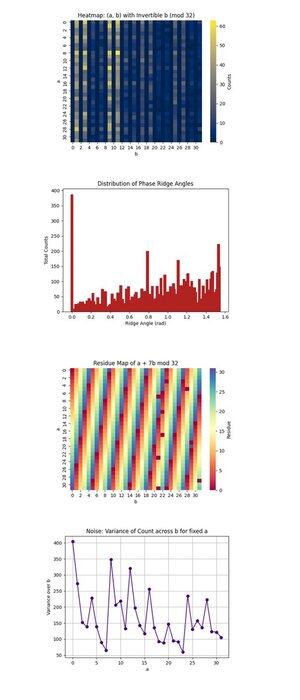Bản đồ Nhiệt: (a, b) với b có thể đảo ngược (mod 32) ở trên (mã đầy đủ trên Qwork) chỉ tập trung vào các cặp (a, b) mà b có thể đảo ngược theo mô-đun 32, một điều kiện cần thiết để phục hồi k. Nó cho thấy nơi sự can thiệp lượng tử đang tập trung trong không gian 1024 điểm. Các vùng cường độ cao tiết lộ các con đường can thiệp ưa thích, gợi ý rằng trạng thái lượng tử phát triển không đồng nhất, có thể ưa chuộng một số quỹ đạo nhất định dưới phép nhân mô-đun. Nó xác nhận độ tương đồng tín hiệu đủ mạnh trong một số vùng để tách biệt các ứng viên hợp lệ. Phân phối của Các Góc Rãnh Pha ở trên (mã đầy đủ trên Qwork) phân loại các góc được hình thành bởi các vector (-a, b) trong mặt phẳng, theo mô-đun π, mà tương ứng với các rãnh pha trong không gian QFT. Các đỉnh trong biểu đồ cho thấy sự căn chỉnh mạnh mẽ, cộng hưởng, của dạng u + kv ≡ 0, có nghĩa là mạch đã mã hóa thành công k vào mẫu can thiệp mặc dù không gian trạng thái đầy đủ rất rộng lớn. Nhiều góc thống trị cho thấy các hài của sự dịch chuyển ẩn đang hiện diện. Bản đồ Dư lượng của a + 7b mod 32 ở trên (mã đầy đủ trên Qwork) hình dung dư lượng đầu ra cho khóa mục tiêu cụ thể k = 7, trên toàn bộ không gian (a, b). Bất kỳ băng hoặc đối xứng nhất quán nào ở đây cho thấy mức độ can thiệp khuếch đại các giải pháp hợp lệ (nơi giá trị này bằng 0). Bạn có thể quan sát các vùng nào của lưới 1024 tương ứng với a + 7b ≡ 0, xác nhận rằng cấu trúc của oracle đã dẫn đến việc in dấu khóa thành công. Tiếng ồn: Phương sai của Số đếm trên b cho a cố định ở trên (mã đầy đủ trên Qwork) cho thấy mức độ ồn hoặc ổn định của các số đếm đầu ra cho mỗi a cố định khi chúng ta thay đổi b. Phương sai cao có nghĩa là một số giá trị b dẫn đến khuếch đại mạnh trong khi những giá trị khác thì không, ngụ ý độ nhạy của mạch hoặc tiếng ồn phía sau cho hàng a đó. Các vùng mượt mà ngụ ý sự đồng bộ lượng tử, trong khi các đỉnh có thể chỉ ra sự mất đồng bộ hoặc sự lan truyền lỗi trong quá trình đánh giá oracle. Cuối cùng, thí nghiệm này đã thành công trong việc phá một khóa đường cong elliptic 5-bit bằng cách sử dụng thuật toán Shor được thực hiện trên bộ xử lý lượng tử 133-qubit của IBM, mở rộng kết quả 4-bit trước đó vào một không gian can thiệp lớn hơn đáng kể (32x32 = 1024 kết quả). Mạch này đã mã hóa oracle qua ℤ₃₂ mà không bao giờ tham chiếu đến số vô hướng bí mật k, và tận dụng số học nhóm mô-đun để ràng buộc số vô hướng vào sự can thiệp pha. Mạch lượng tử, sâu 67,000 lớp, đã tạo ra các mẫu can thiệp hợp lệ mặc dù độ sâu mạch cực kỳ lớn, và xử lý hậu kỳ cổ điển đã tiết lộ k = 7 trong 100 kết quả có thể đảo ngược (a, b) hàng đầu. Thông qua các hình ảnh, thí nghiệm này đã xác nhận các cấu trúc rãnh chéo, mặt nạ có thể đảo ngược, và sự căn chỉnh hài hòa của các rãnh can thiệp, xác nhận rằng sự đồng bộ lượng tử vẫn đủ mạnh để khuếch đại mối quan hệ mô-đun chính xác. Điều này thiết lập rằng thuật toán Shor tiếp tục mở rộng dưới các chế độ mạch sâu hơn và rằng các chiến lược phục hồi khóa dựa trên từ điển (liệt kê 100 hàng đầu) vẫn khả thi khi độ dài bit tăng lên, cho thấy lợi thế lượng tử rõ ràng ngay cả trong các điều kiện thực tế ồn ào. Mã # Mạch chính # Nhập khẩu import logging, json from math import gcd import numpy as np from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile from qiskit.circuit.library import UnitaryGate, QFT from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 import pandas as pd # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SHOTS = 16384 # Tham số đường cong Toy (nhóm con bậc 32 của E(F_p)) ORDER = 32 # |E(F_p)| = 32 P_IDX = 1 # Sinh viên P -> chỉ số 1 Q_IDX = 23 # Điểm công khai Q = kP, ở đây "23 mod 32" cho k = 7 # Trợ giúp ghi nhật ký logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(levelname)s | %(message)s") log = logging.getLogger(__name__) # Chọn qubit dựa trên hiệu chuẩn def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() winners = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascending=[True, False, False]) ["Qubit"].head(n).tolist() ) log .info("Các qubit vật lý tốt nhất: %s", winners) return winners N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, điểm PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL) # Cổng cộng hằng số theo mô-đun 32 như một cổng tái sử dụng def add_const_mod32_gate(c: int) -> UnitaryGate: """Trả về một cổng 5-qubit ánh xạ |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) for x in range(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant): """Áp dụng |x⟩ → |x+constant (mod 32)⟩ được điều khiển bởi một qubit.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (số chỉ mục theo mô-đun 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): for i in range(N_Q): constant = (P_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, a_reg[i], point_reg, constant) for i in range(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Xây dựng toàn bộ mạch Shor def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) return qc # Thực hiện IBM Runtime service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANCE) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=PHYSICAL, optimization_level=3) log .info("Độ sâu mạch %d, số lượng cổng %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) result = job.result() # Xử lý hậu kỳ cổ điển creg_name = trans.cregs[0].name counts_raw = result[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v in counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Tiêu chí thành công. Kiểm tra 100 hàng có thể đảo ngược hàng đầu cho k = 7 top_invertibles = [] for (a_val, b_val), freq in top: if gcd(b_val, ORDER) != 1: continue inv_b = pow(b_val, -1, ORDER) k_candidate = (-a_val * inv_b) % ORDER top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: break # Kiểm tra thành công và in kết quả found_k7 = any(k == 7 for (_, k, _) in top_invertibles) if found_k7: print("\nTHÀNH CÔNG — k = 7 được tìm thấy trong 100 kết quả hàng đầu\n") else: print("\nCẢNH BÁO — k = 7 KHÔNG được tìm thấy trong 100 kết quả hàng đầu\n") print("100 cặp có thể đảo ngược (a, b) hàng đầu và k đã phục hồi:") for (a, b), k, count in top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (số lượng = {count}){tag}") # Lưu dữ liệu thô out = { "thí nghiệm": "ECDLP_32pts_Shors", "backend": backend .name, "qubit vật lý": PHYSICAL, "shots": SHOTS, "counts": counts_raw } JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json" with open(JSON_PATH, "w") as fp: json.dump(out, fp, indent=4) log .info("Kết quả đã lưu → %s", JSON_PATH) # Kết thúc Mã đầy đủ cho tất cả các hình ảnh sử dụng dữ liệu chạy trên Qwork.