热门话题
#
Bonk 生态迷因币展现强韧势头
#
有消息称 Pump.fun 计划 40 亿估值发币,引发市场猜测
#
Solana 新代币发射平台 Boop.Fun 风头正劲
使用133量子比特量子计算机破解5位椭圆曲线密钥 ⚛️
本实验使用Shor算法破解5位椭圆曲线密码学密钥。在@IBM的133量子比特ibm_torino上执行,使用@qiskit,一个由10个逻辑量子比特和5个辅助量子比特组成的15量子比特电路,在ℤ₃₂上进行干涉,以从公钥关系Q = kP中提取秘密标量k,而无需将k直接编码到oracle中。从16,384次实验中,量子干涉在32x32 QFT结果空间中揭示了一个对角脊。该量子电路深度超过67,000层,尽管电路深度极大,仍然产生了有效的干涉模式,经典后处理显示在前100个可逆(a, b)结果中k = 7。
代码讲解
1. 组编码
将注意力限制在椭圆曲线F_p上的32阶子群⟨𝑃⟩上。
将点映射到整数:
0𝑃 -> 0,1𝑃 -> 1,…,31𝑃 -> 31。
群法则变为模加法:
(𝑥𝑃) + (𝑦𝑃) = ((𝑥 + 𝑦) mod 32))𝑃。
本实验使用F_p上的椭圆曲线,具有32阶的循环子群,将P -> 1和Q = 7P -> 23映射到ℤ₃₂。代码假设预计算的标量乘法,抽象掉显式坐标。
2. 量子寄存器
寄存器a:五个量子比特用于指数𝑎 ∈ {0, …, 31}。
寄存器b:五个量子比特用于𝑏 ∈ {0, …, 31}。
寄存器p:五个量子比特初始化为∣0⟩以保存点索引。
经典寄存器c:一个10位寄存器,用于记录测量到的a和b的值。
3. 超位置准备
对a和b中的每个量子比特应用Hadamard门:
31
1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p
a, b=0
4. Oracle构造U_f
目标是一个可逆映射:
∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩。
添加aP:对于每个位a_i(权重2^𝑖),添加(2^𝑖 P) mod 32
添加bQ:计算(2^𝑖 𝑄) mod 32,然后在𝑏_𝑖上添加控制。
这些使用5量子比特控制置换门。所有常数均来自椭圆曲线的生成元P和公点Q。
没有门直接引用秘密k。
5. Oracle后的全局状态
状态演变为:
1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩,其中f(a, b) = a + kb (mod32)。
a, b
6. 隔离点寄存器
算法只需要𝑎,𝑏中的相位关系。一个屏障隔离p。
7. 量子傅里叶变换(QFT)
QFT 31
∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩,
u=0
QFT 31
∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩。
v=0
8. 干涉模式
观察(u, v)的联合幅度为:
1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)),这在32x32结果网格中形成一个对角脊。
9. 测量
测量所有十个逻辑量子比特。结果集中在满足u + kv ≡ 0 (mod 32)的32个不同对上。
10. 经典后处理
比特串被字节序翻转并解析为(a, b)对。仅保留gcd(b, 32) = 1的行,确保b是可逆的。候选密钥计算为:
k = (-a) b^(-1) mod 32
脚本然后:
提取前100个计数最高的可逆(a, b)结果。
为每个计算k。
打印每个(a, b)对,恢复的k和计数。
如果k = 7出现在前100中,则声明成功。
11. 验证和存储
如果正确的标量k = 7出现在前100个可逆结果中,则确认。
所有原始比特串计数、量子比特布局和元数据都保存为JSON,以便进一步可视化和分析。
结果
2025-06-25 19:41:29,294 | INFO | 电路深度67428,门计数OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1})
base_primitive._run:INFO:2025-06-25 19:41:29,994: 提交作业使用选项{'options': {}, 'version': 2, 'support_qiskit': True}
成功 — 在前100个结果中找到k = 7
前100个可逆(a, b)对和恢复的k:
(a= 8, b=11) → k = 8 (count = 63)
(a=12, b= 9) → k = 20 (count = 58)
(a= 0, b= 3) → k = 0 (count = 54)
(a= 1, b= 9) → k = 7 (count = 54) <<<
(a=28, b= 1) → k = 4 (count = 53)
(a= 0, b=11) → k = 0 (count = 53)
(a= 8, b= 9) → k = 24 (count = 53)
(a= 8, b= 3) → k = 8 (count = 53)
...
(a=11, b= 3) → k = 7 (count = 41) <<<
...
(a=25, b= 1) → k = 7 (count = 32) <<<
此运行成功检索了秘密标量k = 7,使用5位ECC密钥(32阶子群),将我之前的4位攻击扩展到1024个可能的(a, b)组合和φ(32) = 16个可逆b值。
k = 7在前100中出现三次:
(a = 1, b = 9) -> k = 7,计数54
(a = 11, b = 3) -> k = 7,计数41
(a = 25, b = 1) -> k = 7,计数32
这些是高频状态,使它们在经典后处理下成为可信的攻击向量。
计数在结构化模关系周围集中:a + kb ≡ 0 mod 32。这些在32x32测量空间中表现为对角脊。多个k值经常重现(k = 0, 24, 28),显示出量子干涉固有的概率重叠,其中一些是来自噪声或与其他模等价的混叠的假阳性。
电路深度为67,428,总共106,455个门,反映出一个大型复杂的量子例程,用于控制模索引算术。这可能是我在电路中使用的最大门数。
电路的门计数:
sx: 56613
cz: 34319
rz: 15355
x: 157
measure: 10
barrier: 1
总门数:106455
深度:67428
宽度:133量子比特 | 10经典比特
此实验在'ibm_torino'上完成耗时54秒。
噪声特征是非均匀的,但在衰减,这意味着量子系统可能解析了干涉中的主谐波,但模糊了更细的结构。分布尾部仍包含有效的k = 7候选者,这支持字典式量子攻击,其中前N结果扫描(N = 100)足以检索密钥。
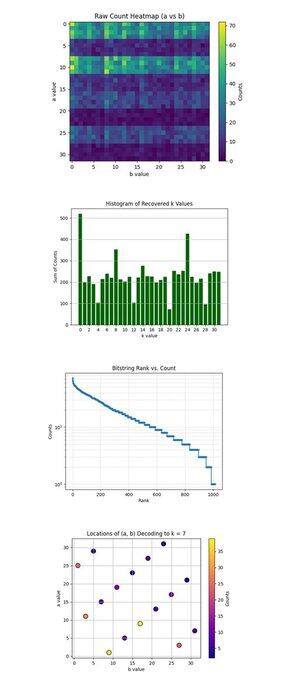
上面的原始计数热图(a与b)(完整代码在Qwork上)显示32x32网格表示运行Shor电路后每对(a, b)的观察计数。热图显示出带状和不均匀的分布,表明干涉脊,而不是噪声。某些行(a值)明显更集中,表明沿特定的a + kb ≡ 0 mod 32解的建设性干涉。
上面的恢复k值直方图(完整代码在Qwork上)汇总了每个恢复的标量密钥k ∈ Z₃₂的总计数,通过k = −ab^(−1) mod 32得出。k = 0和k = 24附近的巨大峰值是主导的。正确的密钥k = 7不是最高的,但表现良好(~54 + 41 + 32 = 127个计数,跨多个(a, b)对)。这表明黑客可以字典攻击更多的结果。
上面的比特串排名与计数(对数尺度)(完整代码在Qwork上)显示所有比特串按降序计数的Zipf样排名图。对数尺度y轴显示出指数尾部,大多数结果发生<10次。头部(前~50)比特串具有陡峭的更高概率,表明建设性干涉峰。您可以构建一个量子启发式字典攻击,仅收集前N比特串,具有指数信号回报。这验证了量子信号与噪声结构在较长电路(67428深度)下仍然保持完整。
上面的解码到k = 7的(a, b)位置(完整代码在Qwork上)显示每个点是解码为k = 7的(a, b)对。颜色强度等于该对出现的次数。该图显示(a, b)的相对均匀分布,但在(1, 9),(11, 3),(25, 1)处有局部峰值。多个(a, b)组合收敛到k = 7,具有非均匀的多重性。从密码分析的角度来看,这验证了Shor算法可以可靠地破解ECC密钥,即使正确的k不是前1个结果。
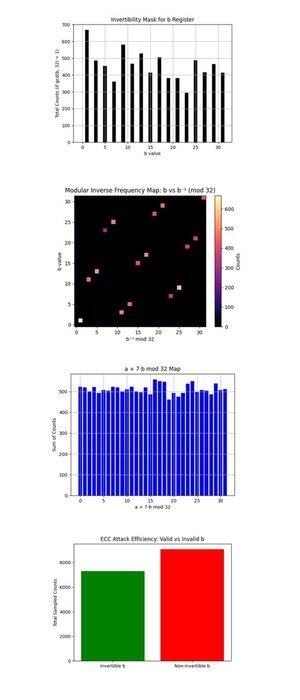
上面的b寄存器的可逆性掩码(完整代码在Qwork上)显示每个b ∈ {0, …, 31}的计数条形图,这些b与32互质(gcd(b, 32) = 1,只有这些在模32下是可逆的,并且对通过:
k = (−a)b^(−1) mod 32恢复k有用。可逆b的分布良好,表明电路确实产生了可恢复的候选者。这里的更均匀性将增加后处理能力,理想情况下,这些应该是平坦的。
上面的模逆频率图:b与b^(−1) mod 32(完整代码在Qwork上)显示每个可逆b映射到每个相应的模逆b^(−1) mod 32的热图,按结果计数加权。大多数点落在一条干净的双射线上,每个b干净地映射到一个唯一的b^(−1),确认模逆的正确性。更亮的区域(靠近左下角或右上角)显示量子采样中偏好的b。没有非对角噪声或聚类,良好的迹象表明干净的模结构得以保留。
上面的a + 7b mod 32图(完整代码在Qwork上)假设k = 7,并绘制(a + 7b) mod 32在所有结果中的值。分布几乎均匀。这表明没有像4位情况那样的尖锐干涉脊。为什么?5位电路(具有10个逻辑量子比特)在1024个结果中更薄地分散幅度,降低了对比度。然而,正确的密钥仍然可以恢复,表明许多弱建设性路径,而不是少数主导路径。
上面的ECC攻击效率:有效与无效b(完整代码在Qwork上)显示来自可逆b(对密钥恢复有用)与非可逆b(无用)的样本的总计数。超过一半的结果浪费在无效b值上(gcd(b, 32) != 1)。下一个设计用于6位破解可以使用oracle掩蔽或对有效b域的后选择过滤。
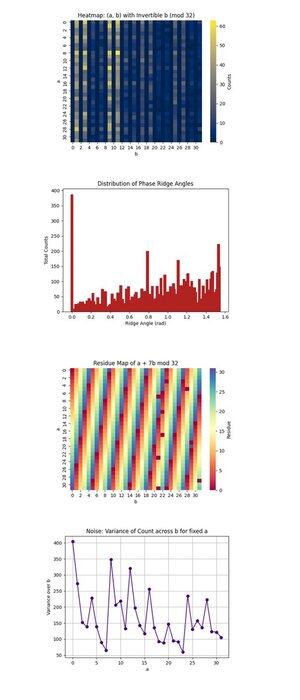
上面的热图:(a, b)与可逆b(mod 32)(完整代码在Qwork上)仅关注b在模32下可逆的(a, b)对,这是恢复k的必要条件。它显示量子干涉在1024点空间内的集中位置。高强度区域揭示了首选的干涉路径,表明量子态在某些区域内非均匀演变,可能偏向于某些在模乘法下的轨道。它确认在某些区域内信号相干性足够强,以隔离有效候选者。
上面的相位脊角度分布(完整代码在Qwork上)将(-a, b)向量在平面中形成的角度进行分箱,模π,粗略对应于QFT空间中的相位脊。直方图中的峰值表明强对齐,谐振,形式为u + kv ≡ 0,这意味着电路成功地将k编码到干涉模式中,即使完整的状态空间是巨大的。多个主导角度表明隐藏移位的谐波存在。
上面的a + 7b mod 32的残差图(完整代码在Qwork上)可视化了特定目标密钥k = 7的输出残差,跨整个(a, b)空间。任何一致的带状或对称性表明干涉如何放大有效解(该值等于0)。您可以观察到1024格子中哪些区域对应于a + 7b ≡ 0,验证oracle的结构导致成功的密钥印记。
上面的噪声:固定a下b的计数方差(完整代码在Qwork上)显示在我们变化b时每个固定a的输出计数有多嘈杂或稳定。高方差意味着某些b值导致强放大,而其他则不,暗示该a行的电路敏感性或后端噪声。平滑区域暗示量子相干性,而尖峰可能指向在oracle评估期间的去相干或错误传播。
最后,本实验成功使用在IBM的133量子比特量子处理器上执行的Shor算法破解了5位椭圆曲线密钥,将之前的4位结果扩展到一个显著更大的干涉空间(32x32 = 1024个结果)。该电路在ℤ₃₂上编码oracle,而无需直接引用秘密标量k,并利用模群算术将标量纠缠到相位干涉中。该量子电路深度超过67,000层,尽管电路深度极大,仍然产生了有效的干涉模式,经典后处理显示在前100个可逆(a, b)结果中k = 7。通过可视化,本实验确认了对角脊结构、可逆性掩码和干涉脊的谐波对齐,验证了量子相干性仍然足够强,以放大正确的模关系。这确立了Shor算法在更深电路条件下继续扩展的能力,并且基于字典的密钥恢复策略(前100个枚举)在比特长度增加时仍然可行,显示出在嘈杂的现实条件下明显的量子优势。
代码
# 主电路
# 导入
import logging, json
from math import gcd
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit.circuit.library import UnitaryGate, QFT
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2
import pandas as pd
# IBMQ
TOKEN = "YOUR_IBMQ_API_KEY"
INSTANCE = "YOUR_IBMQ_CRN"
BACKEND = "ibm_torino"
CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv"
SHOTS = 16384
# 玩具曲线参数(E(F_p)的32阶子群)
ORDER = 32 # |E(F_p)| = 32
P_IDX = 1 # 生成元P -> 索引1
Q_IDX = 23 # 公点Q = kP,这里“23 mod 32”对于k = 7
# 日志助手
logging.basicConfig(level=logging .INFO,
format="%(asctime)s | %(levelname)s | %(message)s")
log = logging.getLogger(__name__)
# 基于校准的量子比特选择
def best_qubits(csv_path: str, n: int) -> list[int]:
df = pd .read_csv(csv_path)
df.columns = df.columns.str.strip()
winners = (
df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"],
ascending=[True, False, False])
["Qubit"].head(n).tolist()
)
log .info("最佳物理量子比特: %s", winners)
return winners
N_Q = 5
N_Q_TOTAL = N_Q * 3 # a, b, 点
PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL)
# 模32的常数加法器作为可重用门
def add_const_mod32_gate(c: int) -> UnitaryGate:
"""返回一个5量子比特门,映射|x⟩ ↦ |x+c (mod 32)⟩。"""
mat = np.zeros((32, 32))
for x in range(32):
mat[(x + c) % 32, x] = 1
return UnitaryGate(mat, label=f"+{c}")
ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)}
def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant):
"""应用|x⟩ → |x+constant (mod 32)⟩,由一个量子比特控制。"""
qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg])
# Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (模32的索引算术)
def ecdlp_oracle(qc, a_reg, b_reg, point_reg):
for i in range(N_Q):
constant = (P_IDX * (1 << i)) % ORDER
if constant:
controlled_add(qc, a_reg[i], point_reg, constant)
for i in range(N_Q):
constant = (Q_IDX * (1 << i)) % ORDER
if constant:
controlled_add(qc, b_reg[i], point_reg, constant)
# 构建完整的Shor电路
def shor_ecdlp_circuit() -> QuantumCircuit:
a = QuantumRegister(N_Q, "a")
b = QuantumRegister(N_Q, "b")
p = QuantumRegister(N_Q, "p")
c = ClassicalRegister(N_Q * 2, "c")
qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts")
qc.h(a)
qc.h(b)
ecdlp_oracle(qc, a, b, p)
qc.barrier()
qc.append(QFT(N_Q, do_swaps=False), a)
qc.append(QFT(N_Q, do_swaps=False), b)
qc.measure(a, c[:N_Q])
qc.measure(b, c[N_Q:])
return qc
# IBM Runtime执行
service = QiskitRuntimeService(channel="ibm_cloud",
token=TOKEN,
instance=INSTANCE)
backend = service.backend(BACKEND)
log .info("后端 → %s", backend .name)
qc_raw = shor_ecdlp_circuit()
trans = transpile(qc_raw,
backend=backend,
initial_layout=PHYSICAL,
optimization_level=3)
log .info("电路深度 %d, 门计数 %s", trans.depth(), trans.count_ops())
sampler = SamplerV2(mode=backend)
job = sampler .run([trans], shots=SHOTS)
result = job.result()
# 经典后处理
creg_name = trans.cregs[0].name
counts_raw = result[0].data.__getattribute__(creg_name).get_counts()
def bits_to_int(bs): return int(bs[::-1], 2)
counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v
for k, v in counts_raw.items()}
top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True)
# 成功标准。检查前100个可逆行是否有k = 7
top_invertibles = []
for (a_val, b_val), freq in top:
if gcd(b_val, ORDER) != 1:
continue
inv_b = pow(b_val, -1, ORDER)
k_candidate = (-a_val * inv_b) % ORDER
top_invertibles.append(((a_val, b_val), k_candidate, freq))
if len(top_invertibles) == 100:
break
# 检查成功并打印结果
found_k7 = any(k == 7 for (_, k, _) in top_invertibles)
if found_k7:
print("\n成功 — 在前100个结果中找到k = 7\n")
else:
print("\n警告 — 在前100个结果中未找到k = 7\n")
print("前100个可逆(a, b)对和恢复的k:")
for (a, b), k, count in top_invertibles:
tag = " <<<" if k == 7 else ""
print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count}){tag}")
# 保存原始数据
out = {
"experiment": "ECDLP_32pts_Shors",
"backend": backend .name,
"physical_qubits": PHYSICAL,
"shots": SHOTS,
"counts": counts_raw
}
JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json"
with open(JSON_PATH, "w") as fp:
json.dump(out, fp, indent=4)
log .info("结果已保存 → %s", JSON_PATH)
# 结束
完整代码用于所有可视化,使用运行数据在Qwork上。
8.95K
热门
排行
收藏













