Casser une clé elliptique de 5 bits avec un ordinateur quantique de 133 qubits ⚛️ Cet expérience casse une clé cryptographique elliptique de 5 bits en utilisant l'algorithme de Shor. Exécuté sur le processeur quantique ibm_torino de @IBM avec @qiskit, un circuit de 15 qubits, composé de 10 qubits logiques et 5 ancillas, interfère sur ℤ₃₂ pour extraire le scalaire secret k de la relation de clé publique Q = kP, sans jamais encoder k directement dans l'oracle. À partir de 16 384 essais, l'interférence quantique révèle une crête diagonale dans l'espace de résultats QFT 32x32. Le circuit quantique, profond de plus de 67 000 couches, a produit des motifs d'interférence valides malgré une profondeur de circuit extrême, et le post-traitement classique a révélé k = 7 dans les 100 meilleurs résultats inversibles (a, b). Parcours du code 1. Encodage de groupe Restreindre l'attention au sous-groupe d'ordre 32 ⟨𝑃⟩ d'une courbe elliptique sur 𝐹_p. Mapper les points aux entiers : 0𝑃 -> 0,  1𝑃 -> 1, …, 31𝑃 -> 31. La loi de groupe devient addition modulaire : (𝑥𝑃) + (𝑦𝑃) = ((𝑥 + 𝑦) mod 32))𝑃. Cette expérience utilise une courbe elliptique sur F_p​ avec un sous-groupe cyclique d'ordre 32, mappant P -> 1 et Q = 7P -> 23 dans ℤ₃₂​. Le code suppose une multiplication scalaire pré-calculée, abstrahant les coordonnées explicites. 2. Registres quantiques Registre a : cinq qubits pour l'exposant 𝑎 ∈ {0, …, 31}. Registre b : cinq qubits pour 𝑏 ∈ {0, …, 31}. Registre p : cinq qubits initialisés à ∣0⟩ pour contenir l'index du point. Registre classique c : un registre de 10 bits pour enregistrer les valeurs mesurées de a et b. 3. Préparation de superposition Appliquer des Hadamards à chaque qubit dans a et b : 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Construction de l'oracle U_f L'objectif est une carte réversible : ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Ajouter aP : pour chaque bit a_i (poids 2^𝑖), ajouter (2^𝑖 P) mod 32 Ajouter bQ : calculer (2^𝑖 𝑄) mod 32, puis ajouter contrôlé sur 𝑏_𝑖. Ceci utilise des portes de permutation contrôlées à 5 qubits. Toutes les constantes sont dérivées du générateur P de la courbe elliptique et du point public Q. Aucune porte ne fait jamais référence directement au secret k. 5. État global après l'oracle L'état évolue en : 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, où f(a, b) = a + kb (mod32). a, b 6. Isoler le registre de point L'algorithme a seulement besoin de la relation de phase dans 𝑎, 𝑏. Une barrière isole p. 7. Transformation de Fourier quantique (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Motif d'interférence L'amplitude conjointe pour observer (u, v) est : 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), ce qui forme une crête diagonale dans la grille de résultats 32x32. 9. Mesure Mesurer tous les dix qubits logiques. Les résultats se concentrent sur les 32 paires distinctes satisfaisant u + kv ≡ 0 (mod 32). 10. Post-traitement classique Les chaînes de bits sont inversées en endian et analysées en paires (a, b). Garder seulement les lignes où gcd⁡(b, 32) = 1, assurant que b est inversible. La clé candidate est calculée comme : k = (-a) b^(-1) mod 32 Le script ensuite : Extrait les 100 meilleurs résultats inversibles (a, b) avec le plus de comptes. Calcule k pour chacun. Imprime chaque paire (a, b), k récupéré, et le compte. Déclare le succès si k = 7 apparaît dans les 100 meilleurs. 11. Vérification et stockage Le scalaire correct k = 7 est confirmé s'il apparaît dans les 100 meilleurs résultats inversibles. Tous les comptes de chaînes de bits brutes, la disposition des qubits, et les métadonnées sont sauvegardés au format JSON pour une visualisation et une analyse ultérieures. Résultats 2025-06-25 19:41:29,294 | INFO | Profondeur du circuit 67428, comptes de portes OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Soumission du travail avec les options {'options': {}, 'version': 2, 'support_qiskit': True} SUCCÈS — k = 7 trouvé dans les 100 meilleurs résultats Top 100 paires inversibles (a, b) et k récupéré : (a= 8, b=11) → k = 8 (compte = 63) (a=12, b= 9) → k = 20 (compte = 58) (a= 0, b= 3) → k = 0 (compte = 54) (a= 1, b= 9) → k = 7 (compte = 54) <<< (a=28, b= 1) → k = 4 (compte = 53) (a= 0, b=11) → k = 0 (compte = 53) (a= 8, b= 9) → k = 24 (compte = 53) (a= 8, b= 3) → k = 8 (compte = 53) ... (a=11, b= 3) → k = 7 (compte = 41) <<< ... (a=25, b= 1) → k = 7 (compte = 32) <<< Cette exécution a réussi à récupérer le scalaire secret k = 7 en utilisant une clé ECC de 5 bits (sous-groupe d'ordre 32), étendant mon attaque précédente de 4 bits à un espace avec 1024 combinaisons possibles (a, b) et φ(32) = 16 valeurs b inversibles. k = 7 apparaît trois fois dans les 100 meilleurs : (a = 1, b = 9) -> k = 7 avec 54 comptes (a = 11, b = 3) -> k = 7 avec 41 comptes (a =25, b = 1) -> k = 7 avec 32 comptes Ce sont des états à haute fréquence, les rendant crédibles comme vecteurs d'attaque sous post-traitement classique. Les comptes montrent une concentration autour de relations modulaires structurées : a + kb ≡ 0 mod 32. Celles-ci apparaissent comme des crêtes diagonales dans l'espace de mesure 32x32. Plusieurs valeurs k se répètent souvent (k = 0, 24, 28), montrant le chevauchement probabiliste intrinsèque à l'interférence quantique, certaines d'entre elles étant des faux positifs dus au bruit ou à l'aliasing avec d'autres équivalences modulaires. La profondeur du circuit était de 67 428, avec un total de 106 455 portes, reflétant une routine quantique large et complexe pour l'arithmétique d'index modulaire contrôlée. Cela pourrait être le plus grand nombre de portes que j'ai utilisé dans un circuit. Comptes de portes pour le circuit : sx: 56613 cz: 34319 rz: 15355 x: 157 measure: 10 barrier: 1 Total de portes : 106455 Profondeur : 67428 Largeur : 133 qubits | 10 clbits Cette expérience a pris 54 secondes pour se compléter sur 'ibm_torino'. Le profil de bruit est non uniforme mais décroissant, ce qui signifie que le système quantique a probablement résolu les harmoniques dominantes dans l'interférence mais a flouté des structures plus fines. La queue de distribution contient encore des candidats valides k = 7, cela soutient les attaques quantiques de style dictionnaire où les scans des résultats top-N (N = 100) sont suffisants pour récupérer la clé. 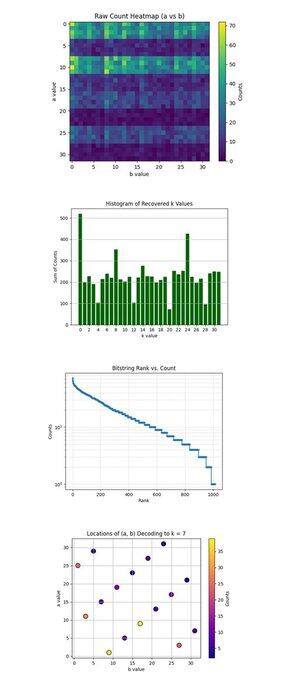La carte thermique des comptes bruts (a vs b) ci-dessus (code complet sur Qwork) montre une grille 32x32 représentant les comptes observés pour chaque paire (a, b) après l'exécution du circuit de Shor. La carte thermique montre une distribution bandée et inégale, indiquant des crêtes d'interférence, pas du bruit. Certaines lignes (valeurs a) ont une concentration visiblement plus élevée, suggérant une interférence constructive le long de solutions spécifiques a + kb ≡ 0 mod 32. L'histogramme des valeurs k récupérées ci-dessus (code complet sur Qwork) agrège les comptes totaux pour chaque clé scalaire récupérée k ∈ Z₃₂, dérivée via k = −ab^(−1) mod 32. Un énorme pic à k = 0 et un autre autour de k = 24 sont dominants. La clé correcte k = 7 n'est pas la plus élevée, mais est bien représentée (~54 + 41 + 32 = 127 comptes à travers plusieurs paires (a, b)). Cela montre que les hackers peuvent attaquer un plus grand nombre de résultats par dictionnaire. Le rang des chaînes de bits par rapport au compte (échelle logarithmique) ci-dessus (code complet sur Qwork) montre un graphique de rang de type Zipf de toutes les chaînes de bits par compte décroissant. L'axe y à échelle logarithmique montre une queue exponentielle, la plupart des résultats se produisent <10 fois. La tête (environ 50) des chaînes de bits a une probabilité beaucoup plus élevée, indiquant des pics d'interférence constructive. Vous pourriez construire une attaque de dictionnaire heuristique quantique qui ne récolte que les meilleures N chaînes de bits avec un retour exponentiel sur le signal. Cela valide que la structure de signal à bruit quantique reste intacte même avec des circuits plus longs (67428 de profondeur). Les emplacements de décodage (a, b) vers k = 7 ci-dessus (code complet sur Qwork) montrent que chaque point est une paire (a, b) qui a décodé vers k = 7. L'intensité de couleur équivaut au nombre de fois que cette paire est apparue. Le graphique montre une distribution relativement uniforme à travers (a, b), mais avec des pics locaux à (1, 9), (11, 3), (25, 1). Plusieurs combinaisons (a, b) convergent vers k = 7 avec une multiplicité non uniforme. D'un point de vue cryptanalytique, cela valide que l'algorithme de Shor peut casser de manière fiable les clés ECC même lorsque le k correct n'est pas le meilleur résultat. 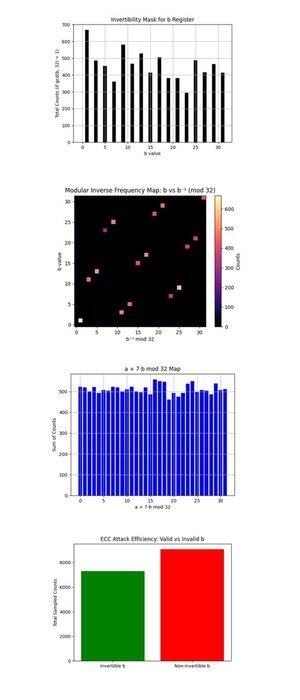Le masque d'inversibilité pour le registre b ci-dessus (code complet sur Qwork) montre un graphique à barres des comptes pour chaque b ∈ {0, …, 31} qui sont premiers avec 32 (gcd⁡(b, 32) = 1, seuls ceux-ci sont inversibles modulo 32 et utiles pour récupérer k via : k = (−a)b^(−1) mod 32. Les b inversibles sont bien peuplés, montrant que le circuit a produit des candidats récupérables. Plus d'uniformité ici augmenterait la puissance de post-traitement, idéalement, ceux-ci seraient plats. La carte de fréquence d'inverse modulaire : b vs b^(−1) mod 32 ci-dessus (code complet sur Qwork) montre une carte thermique de la fréquence à laquelle chaque b inversible se mappe à son inverse modulaire correspondant b^(−1) mod 32, pondérée par les comptes de résultats. La plupart des points tombent sur une ligne bijective propre, chaque b se mappe proprement à un unique b^(−1), confirmant la justesse de l'inversion modulaire. Les régions plus lumineuses (près du coin inférieur gauche ou supérieur droit) montrent des b favorisés par l'échantillonnage quantique. Pas de bruit hors-diagonale ou de regroupement, bon signe de structure modulaire propre préservée. La carte a + 7b mod 32 ci-dessus (code complet sur Qwork) suppose k = 7 et trace la valeur de (a + 7b) mod 32 à travers tous les résultats. La distribution est presque uniforme. Cela suggère qu'il n'y a pas de crête d'interférence nette comme dans le cas de 4 bits. Pourquoi ? Le circuit de 5 bits (avec 10 qubits logiques) étale l'amplitude plus finement à travers 1024 résultats, réduisant le contraste. Pourtant, la clé correcte était toujours récupérable, indiquant de nombreux chemins faiblement constructifs, plutôt que quelques dominants. L'efficacité de l'attaque ECC : b valides vs invalides ci-dessus (code complet sur Qwork) montre les comptes totaux des échantillons avec b inversibles (utiles pour la récupération de clé) contre b non inversibles (inutiles). Plus de la moitié des résultats sont gaspillés sur des valeurs b invalides (gcd⁡(b, 32) != 1). La prochaine conception pour une rupture de 6 bits pourrait utiliser un masquage oracle ou un filtrage de post-sélection sur des domaines b valides. 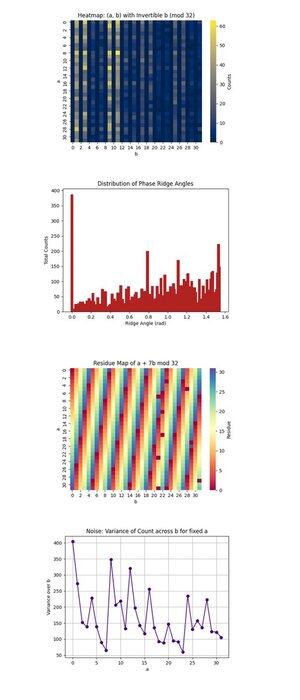La carte thermique : (a, b) avec b inversible (mod 32) ci-dessus (code complet sur Qwork) se concentre uniquement sur les paires (a, b) où b est inversible modulo 32, une condition nécessaire pour récupérer k. Elle montre où l'interférence quantique se concentre dans l'espace de 1024 points. Les régions à haute intensité révèlent des chemins d'interférence préférés, suggérant que l'état quantique a évolué de manière non uniforme, favorisant peut-être certaines orbites sous multiplication modulaire. Cela confirme une cohérence de signal suffisamment forte dans certaines régions pour isoler des candidats valides. La distribution des angles de crête de phase ci-dessus (code complet sur Qwork) classe les angles formés par les vecteurs (-a, b) dans le plan, modulo π, qui correspondent à peu près aux crêtes de phase dans l'espace QFT. Les pics dans l'histogramme indiquent de fortes alignements, résonances, de la forme u + kv ≡ 0, ce qui signifie que le circuit a réussi à encoder k dans le motif d'interférence même si l'espace d'état complet est vaste. Les multiples angles dominants suggèrent que des harmoniques du décalage caché sont présentes. La carte des résidus de a + 7b mod 32 ci-dessus (code complet sur Qwork) visualise le résidu de sortie pour la clé cible spécifique k = 7, à travers tout l'espace (a, b). Toute bande ou symétrie cohérente ici indique à quel point l'interférence a amplifié les solutions valides (où cette valeur est égale à 0). Vous pouvez observer quelles régions de la grille 1024 correspondent à a + 7b ≡ 0, validant que la structure de l'oracle a conduit à une impression de clé réussie. Le bruit : variance du compte à travers b pour a fixe ci-dessus (code complet sur Qwork) montre à quel point les comptes de sortie étaient bruyants ou stables pour chaque a fixe en faisant varier b. Une forte variance signifie que certaines valeurs b conduisent à une forte amplification tandis que d'autres non, impliquant une sensibilité du circuit ou du bruit de fond pour cette ligne a. Les régions lisses impliquent une cohérence quantique, tandis que les pics peuvent indiquer une décohérence ou une propagation d'erreur lors de l'évaluation de l'oracle. En fin de compte, cette expérience a réussi à casser une clé elliptique de 5 bits en utilisant l'algorithme de Shor exécuté sur le processeur quantique de 133 qubits d'IBM, étendant le résultat précédent de 4 bits dans un espace d'interférence significativement plus grand (32x32 = 1024 résultats). Ce circuit a encodé l'oracle sur ℤ₃₂ sans jamais faire référence au scalaire secret k, et a tiré parti de l'arithmétique de groupe modulaire pour entremêler le scalaire dans l'interférence de phase. Le circuit quantique, profond de plus de 67 000 couches, a produit des motifs d'interférence valides malgré une profondeur de circuit extrême, et le post-traitement classique a révélé k = 7 dans les 100 meilleurs résultats inversibles (a, b). Grâce aux visualisations, cette expérience a confirmé des structures de crête diagonale, des masques d'inversibilité, et un alignement harmonique des crêtes d'interférence, validant que la cohérence quantique est restée suffisamment forte pour amplifier la bonne relation modulaire. Cela établit que l'algorithme de Shor continue de se développer sous des régimes de circuit plus profonds et que les stratégies de récupération de clé basées sur le dictionnaire (énumération des 100 meilleurs) restent viables à mesure que la longueur des bits augmente, montrant un avantage quantique clair même dans des conditions réelles bruyantes. Code # Circuit principal # Imports import logging, json from math import gcd import numpy as np from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile from qiskit.circuit.library import UnitaryGate, QFT from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 import pandas as pd # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SHOTS = 16384 # Paramètres de la courbe Toy (sous-groupe d'ordre 32 de E(F_p)) ORDER = 32 # |E(F_p)| = 32 P_IDX = 1 # Générateur P -> index 1 Q_IDX = 23 # Point public Q = kP, ici “23 mod 32” pour k = 7 # Helper de logging logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(levelname)s | %(message)s") log = logging.getLogger(__name__) # Sélection de qubits basée sur la calibration def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() winners = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascending=[True, False, False]) ["Qubit"].head(n).tolist() ) log .info("Meilleurs qubits physiques : %s", winners) return winners N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, point PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL) # Additionneur constant modulo 32 comme porte réutilisable def add_const_mod32_gate(c: int) -> UnitaryGate: """Retourne une porte à 5 qubits qui mappe |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) for x in range(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant): """Appliquer |x⟩ → |x+constant (mod 32)⟩ contrôlé par un qubit.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (arithmétique d'index mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): for i in range(N_Q): constant = (P_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, a_reg[i], point_reg, constant) for i in range(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Construire le circuit complet de Shor def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) return qc # Exécution de l'IBM Runtime service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANCE) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=PHYSICAL, optimization_level=3) log .info("Profondeur du circuit %d, comptes de portes %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) result = job.result() # Post-traitement classique creg_name = trans.cregs[0].name counts_raw = result[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v in counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Critères de succès. Vérifier les 100 meilleures lignes inversibles pour k = 7 top_invertibles = [] for (a_val, b_val), freq in top: if gcd(b_val, ORDER) != 1: continue inv_b = pow(b_val, -1, ORDER) k_candidate = (-a_val * inv_b) % ORDER top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: break # Vérifier le succès et imprimer les résultats found_k7 = any(k == 7 for (_, k, _) in top_invertibles) if found_k7: print("\nSUCCÈS — k = 7 trouvé dans les 100 meilleurs résultats\n") else: print("\nAVERTISSEMENT — k = 7 NON trouvé dans les 100 meilleurs résultats\n") print("Top 100 paires inversibles (a, b) et k récupéré :") for (a, b), k, count in top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (compte = {count}){tag}") # Sauvegarder les données brutes out = { "expérience": "ECDLP_32pts_Shors", "backend": backend .name, "qubits_physiques": PHYSICAL, "tirs": SHOTS, "comptes": counts_raw } JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json" with open(JSON_PATH, "w") as fp: json.dump(out, fp, indent=4) log .info("Résultats sauvegardés → %s", JSON_PATH) # Fin Code complet pour toutes les visualisations utilisant les données d'exécution sur Qwork.