Quebrando uma chave de curva elíptica de 5 bits com um computador ⚛️ quântico de 133 qubits Este experimento quebra uma chave criptográfica de curva elíptica de 5 bits usando o algoritmo de Shor. Executado no ibm_torino de 133 qubits do @IBM com @qiskit, um circuito de 15 qubits, composto por 10 qubits lógicos e 5 ancilla, interfere em Z₃₂ para extrair o escalar secreto k da relação de chave pública Q = kP, sem nunca codificar k diretamente no oráculo. A partir de 16.384 disparos, a interferência quântica revela uma crista diagonal no espaço de resultado de 32x32 QFT. O circuito quântico, com mais de 67.000 camadas de profundidade, produziu padrões de interferência válidos, apesar da extrema profundidade do circuito, e o pós-processamento clássico revelou k = 7 nos 100 principais resultados invertíveis (a, b). Passo a passo do código 1. Codificação de grupo Restrinja a atenção ao subgrupo de ordem 32 ⟨P⟩ de uma curva elíptica sobre F_p. O mapa aponta para números inteiros: 0P -> 0, 1P -> 1, ..., 31P -> 31. A lei de grupo torna-se uma adição modular: (xP) + (yP) = ((x + y) mod 32))P. Este experimento usa uma curva elíptica sobre F_p com um subgrupo cíclico de ordem 32, mapeando P -> 1 e Q = 7P -> 23 em Z₃₂. O código pressupõe multiplicação escalar pré-computada, abstraindo coordenadas explícitas. 2. Registros quânticos Registre a: cinco qubits para o expoente a ∈ {0, ..., 31}. Registro b: cinco qubits para b ∈ {0, ..., 31}. Registre p: cinco qubits inicializados para ∣0⟩ para manter o índice de pontos. Registrador clássico c: um registrador de 10 bits para registrar os valores medidos de a e b. 3. Preparação de superposição Aplique Hadamards a cada qubit em a e b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. U_f de construção do Oracle O objetivo é um mapa reversível: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Adicione aP: para cada bit a_i (peso 2^i), adicione (2^i P) mod 32 Adicione bQ: compute (2 ^ i Q) mod 32 e, em seguida, adicione controlado em b_i. Eles usam portas de permuta controladas por 5 qubits. Todas as constantes são derivadas do gerador P da curva elíptica e do ponto público Q. Nenhuma porta faz referência direta ao segredo k. 5. Estado global após o Oracle O estado evolui para: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, onde f(a, b) = a + kb (mod32). a, b 6. Isolar Registro de Pontos O algoritmo precisa apenas da relação de fase em a, b. Uma barreira isola p. 7. Transformada quântica de Fourier (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u = 0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Padrão de interferência A amplitude da junta para observação (u, v) é: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), que forma uma crista diagonal na grade de resultados 32x32. 9. Medição Meça todos os dez qubits lógicos. Os resultados concentram-se nos 32 pares distintos que satisfazem u + kv ≡ 0 (mod 32). 10. Pós-processamento clássico As cadeias de bits são invertidas em endian e analisadas em pares (a, b). Mantenha apenas as linhas em que gcd(b, 32) = 1, garantindo que b seja invertível. A chave candidata é calculada como: k = (-a) b^(-1) mod 32 O script então: Extrai os 100 principais resultados invertíveis (a, b) de contagem mais alta. Calcula k para cada um. Imprime cada par (a, b), k recuperado e conta. Declara êxito se k = 7 aparecer entre os 100 primeiros. 11. Verificação e armazenamento O escalar correto k = 7 é confirmado se aparecer nos 100 principais resultados invertíveis. Todas as contagens brutas de cadeia de bits, layout de qubit e metadados são salvos em JSON para visualização e análise adicionais. Resultados 2025-06-25 19:41:29,294 | INFORMAÇÕES | Profundidade do circuito 67428, contagens de portas OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'medida': 10, 'barreira': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Enviando trabalho usando as opções {'options': {}, 'version': 2, 'support_qiskit': True} SUCESSO — k = 7 encontrado nos 100 melhores resultados Os 100 principais pares invertíveis (a, b) e k recuperados: (a = 8, b = 11) → k = 8 (contagem = 63) (a=12, b= 9) → k = 20 (contagem = 58) (a= 0, b= 3) → k = 0 (contagem = 54) (a= 1, b= 9) → k = 7 (contagem = 54) <<< (a=28, b= 1) → k = 4 (contagem = 53) (a= 0, b=11) → k = 0 (contagem = 53) (a= 8, b= 9) → k = 24 (contagem = 53) (a= 8, b= 3) → k = 8 (contagem = 53) ... (a=11, b= 3) → k = 7 (contagem = 41) <<< ... (a=25, b= 1) → k = 7 (contagem = 32) <<< Esta execução recuperou com sucesso o escalar secreto k = 7 usando uma chave ECC de 5 bits (subgrupo de ordem 32), estendendo meu ataque anterior de 4 bits para um espaço com 1024 combinações possíveis (a, b) e φ(32) = 16 valores b invertíveis. k = 7 aparece três vezes no top 100: (a = 1, b = 9) -> k = 7 com 54 contagens (a = 11, b = 3) -> k = 7 com 41 contagens (a = 25, b = 1) -> k = 7 com 32 contagens Esses são estados de alta frequência, tornando-os vetores de ataque confiáveis no pós-processamento clássico. As contagens exibem concentração em torno de relações modulares estruturadas: a + kb ≡ 0 mod 32. Eles aparecem como cristas diagonais no espaço de medição de 32x32. Vários valores k se repetem com frequência (k = 0, 24, 28), mostrando a sobreposição probabilística intrínseca à interferência quântica, alguns deles são falsos positivos de ruído ou aliasing com outras equivalências modulares. A profundidade do circuito foi de 67.428, com um total de 106.455 portas, refletindo uma rotina quântica grande e complexa para aritmética de índice modular controlado. Esta pode ser a maior quantidade de portas que usei em um circuito. Contagens de portas para o circuito: SX: 56613 CZ: 34319 RZ: 15355 X: 157 medida: 10 barreira: 1 Total de portões: 106455 Profundidade: 67428 Largura: 133 qubits | 10 clbits Este experimento levou 54 segundos para ser concluído em 'ibm_torino'. O perfil de ruído não é uniforme, mas decai, o que significa que o sistema quântico provavelmente resolveu harmônicos dominantes na interferência, mas borrou estruturas mais finas. A cauda de distribuição ainda contém k = 7 candidatos válidos, isso dá suporte a ataques quânticos no estilo de dicionário em que as verificações de resultados dos N principais (N = 100) são suficientes para recuperar a chave. 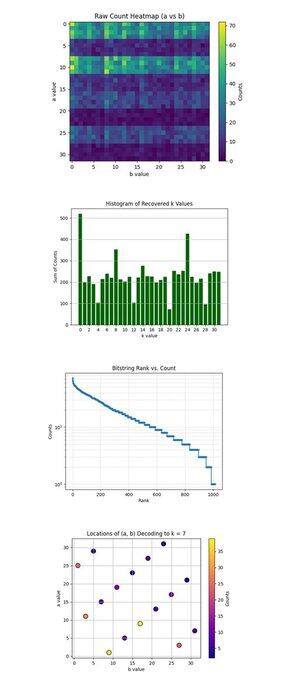O mapa de calor de contagem bruta (a vs b) acima (código completo no Qwork) mostra que uma grade de 32x32 representa as contagens observadas para cada par (a, b) após a execução do circuito de Shor. O mapa de calor mostra uma distribuição em faixas e desigual, indicando sulcos de interferência, não ruído. Certas linhas (valores a) têm concentração visivelmente mais alta, sugerindo interferência construtiva ao longo de soluções específicas a + kb ≡ 0 mod 32. O Histograma de Valores k Recuperados acima (código completo em Qwork) agrega as contagens totais para cada chave escalar recuperada k ∈ Z₃₂, derivada via k = −ab^(−1) mod 32. Um grande pico em k = 0 e outro em torno de k = 24 são dominantes. A chave correta k = 7 não é a mais alta, mas está bem representada (~ 54 + 41 + 32 = 127 contagens em vários pares (a, b)). Isso mostra que os hackers podem atacar uma quantidade maior de resultados. O Bitstring Rank vs Count (Log-Scale) acima (código completo no Qwork) mostra um gráfico de classificação semelhante ao Zipf de todas as strings de bits por contagem decrescente. O eixo y da escala logarítmica mostra uma cauda exponencial, a maioria dos resultados ocorre <10 vezes. As cadeias de bits de cabeçote (superior ~50) têm probabilidade muito maior, indicando picos de interferência construtiva. Você pode criar um ataque de dicionário heurístico quântico que coleta apenas as N principais cadeias de bits com retorno exponencial no sinal. Isso valida que a estrutura quântica sinal-ruído ainda está intacta, mesmo com circuitos mais longos (profundidade 67428). Os locais de (a, b) Decodificando para k = 7 acima (código completo no Qwork) mostram que cada ponto é um par (a, b) que decodificou para k = 7. A intensidade da cor é igual ao número de vezes que esse par ocorreu. O gráfico mostra uma distribuição relativamente uniforme em (a, b), mas com picos locais em (1, 9), (11, 3), (25, 1). Múltiplas combinações (a, b) convergem para k = 7 com multiplicidade não uniforme. Do ponto de vista criptoanalítico, isso valida que o algoritmo de Shor pode quebrar chaves ECC de forma confiável, mesmo quando o k correto não é o resultado 1 principal. 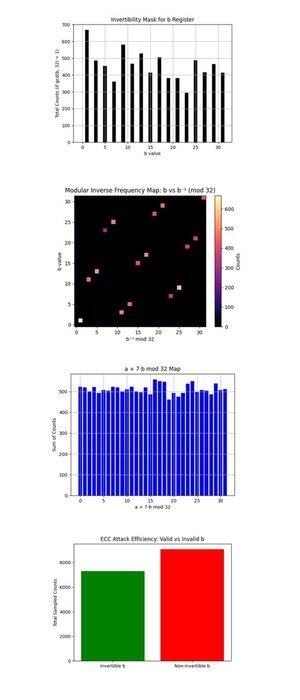A Máscara de Invertibilidade para b Registro acima (código completo em Qwork) mostra um gráfico de barras de contagens para cada b ∈ {0, ..., 31} que são coprimos com 32 (gcd(b, 32) = 1, apenas estes são módulo invertível 32 e úteis para recuperar k via: k = (−a)b^(−1) mod 32. Os b's invertíveis são bem povoados, mostrando que o circuito produziu candidatos recuperáveis. Mais uniformidade aqui aumentaria o poder de pós-processamento, idealmente, eles seriam planos. O Mapa de Frequência Inversa Modular: b vs b^(−1) mod 32 acima (código completo no Qwork) mostra um mapa de calor de quantas vezes cada b invertível mapeia para cada inverso modular b^(−1) mod 32 correspondente, ponderado pela contagem de resultados. A maioria dos pontos cai em uma linha bijetiva limpa, cada b mapeia de forma limpa para um único b ^ (−1), confirmando a exatidão da inversão modular. Regiões mais brilhantes (perto do canto inferior esquerdo ou superior direito) mostram b's favorecidos da amostragem quântica. Sem ruído fora da diagonal ou agrupamento, bom sinal de estrutura modular limpa preservada. O mapa a + 7b mod 32 acima (código completo no Qwork) assume k = 7 e plota o valor de (a + 7b) mod 32 em todos os resultados. A distribuição é quase uniforme. Isso sugere que não há uma crista de interferência nítida como no caso de 4 bits. Por que? O circuito de 5 bits (com 10 qubits lógicos) espalha a amplitude mais fina em 1024 resultados, reduzindo o contraste. No entanto, a chave correta ainda era recuperável, indicando muitos caminhos fracamente construtivos, em vez de alguns dominantes. A Eficiência de Ataque ECC: Válido vs Inválido b acima (código completo no Qwork) mostra contagens totais de amostras com b invertível (útil para recuperação de chave) vs. b não invertível (inútil). Mais da metade dos resultados são desperdiçados em valores b inválidos (gcd(b, 32) != 1). O próximo design para uma quebra de 6 bits pode usar mascaramento de oráculo ou filtragem pós-seleção em domínios b válidos. 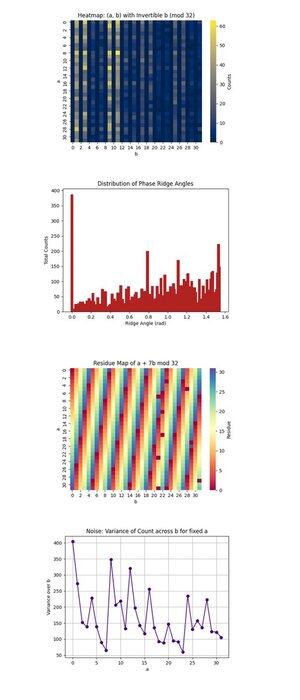O Mapa de Calor: (a, b) com Invertível b (mod 32) acima (código completo no Qwork) concentra-se apenas em (a, b) pares onde b é o módulo invertível 32, uma condição necessária para recuperar k. Ele mostra onde a interferência quântica está se concentrando dentro do espaço de 1024 pontos. As regiões de alta intensidade revelam caminhos de interferência preferidos, sugerindo que o estado quântico evoluiu de maneira não uniforme, possivelmente favorecendo certas órbitas sob multiplicação modular. Ele confirma a coerência de sinal forte o suficiente em algumas regiões para isolar candidatos válidos. A Distribuição dos Ângulos de Crista de Fase acima (código completo em Qwork) agrupa os ângulos formados por (-a, b) vetores no plano, módulo π, que correspondem aproximadamente a cristas de fase no espaço QFT. Picos no histograma indicam fortes alinhamentos, ressonâncias, da forma u + kv ≡ 0, o que significa que o circuito codificou k com sucesso no padrão de interferência, embora o espaço de estado completo seja vasto. Os múltiplos ângulos dominantes sugerem que harmônicos do deslocamento oculto estão presentes. O Mapa de Resíduo de um + 7b mod 32 acima (código completo no Qwork) visualiza o resíduo de saída para a chave de destino específica k = 7, em todo o espaço (a, b). Quaisquer bandas ou simetrias consistentes aqui indicam quão bem a interferência amplificou soluções válidas (onde esse valor é igual a 0). Você pode observar quais regiões da rede 1024 correspondem a + 7b ≡ 0, validando que a estrutura do oráculo levou a uma impressão de chave bem-sucedida. O Ruído: Variância da Contagem em b para o fixo a acima (código completo no Qwork) mostra o quão ruidosas ou estáveis foram as contagens de saída para cada fixo a à medida que variamos b. Alta variância significa que alguns valores b levam a uma forte amplificação, enquanto outros não, implicando sensibilidade do circuito ou ruído de back-end para essa linha a. Regiões suaves implicam coerência quântica, enquanto picos podem apontar para decoerência ou propagação de erros durante a avaliação do oráculo. No final, esse experimento quebrou com sucesso uma chave de curva elíptica de 5 bits usando o algoritmo de Shor executado no processador quântico de 133 qubits da IBM, estendendo o resultado anterior de 4 bits para um espaço de interferência significativamente maior (32x32 = 1024 resultados). Este circuito codificou o oráculo sobre Z₃₂ sem nunca fazer referência ao escalar secreto k, e alavancou a aritmética de grupo modular para emaranhar o escalar em interferência de fase. O circuito quântico, com mais de 67.000 camadas de profundidade, produziu padrões de interferência válidos, apesar da extrema profundidade do circuito, e o pós-processamento clássico revelou k = 7 nos 100 principais resultados invertíveis (a, b). Por meio de visualizações, esse experimento confirmou estruturas de cristas diagonais, máscaras de invertibilidade e alinhamento harmônico de cristas de interferência, validando que a coerência quântica permaneceu forte o suficiente para amplificar a relação modular correta. Isso estabelece que o algoritmo de Shor continua a escalar sob regimes de circuito mais profundos e que as estratégias de recuperação de chave baseadas em dicionário (enumeração top 100) permanecem viáveis à medida que o comprimento de bits aumenta, mostrando uma clara vantagem quântica mesmo sob condições ruidosas do mundo real. Código # Circuito principal # Importações registro de importação, json De importação de matemática GCD importar numpy como np de qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile de qiskit.circuit.library import UnitaryGate, QFT de qiskit_ibm_runtime importar QiskitRuntimeService, SamplerV2 importar pandas como pd # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTÂNCIA = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Usuários/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" TIROS = 16384 # Parâmetros da curva de brinquedo (subgrupo de ordem 32 de E(F_p)) ORDEM = 32 # |E(F_p)| = 32 P_IDX = 1 # Gerador P -> índice 1 Q_IDX = 23 # Ponto público Q = kP, aqui "23 mod 32" para k = 7 # Auxiliar de registro logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(nomedonível)s | %(mensagem)s") log = logging.getLogger(__name__) # Escolha de qubit baseada em calibração def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() vencedores = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascending=[Verdadeiro, Falso, Falso]) ["Qubit"].head(n).tolist() ) log .info("Melhores qubits físicos: %s", vencedores) Vencedores de retorno N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, ponto FÍSICO = best_qubits(CAL_CSV, N_Q_TOTAL) # Somador constante módulo 32 como uma porta reutilizável def add_const_mod32_gate(c: int) -> UnitaryGate: """Retorna uma porta de 5 qubits que mapeia |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) para x no intervalo (32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) para c no intervalo(1, 32)} def controlled_add(qc: CircuitoQuântico, ctrl_qubit, point_reg, constante): """Aplicar |x⟩ → |x+constante (mod 32)⟩ controlada por um qubit.""" qc.append(ADDERS[constante].control(), [ctrl_qubit, *point_reg]) # Oráculo U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (índice aritmético mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): para i no intervalo(N_Q): constante = (P_IDX * (1 << i)) % ORDEM Se constante: controlled_add(qc, a_reg[i], point_reg, constante) para i no intervalo(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Constrói o circuito Shor completo def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = CircuitoQuântico(a, b, p, c, nome="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(QC, A, B, P) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) retorno qc # Execução do IBM Runtime serviço = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTÂNCIA) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpilar(qc_raw, backend = backend, initial_layout = FÍSICO, optimization_level=3) log .info("Profundidade do circuito %d, contagens de portas %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) resultado = job.result() # Pós-processamento clássico creg_name = trans.cregs[0].name counts_raw = resultado[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) contagens = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v para k, v em counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Critérios de sucesso. Verifique as 100 principais linhas invertíveis para k = 7 top_invertibles = [] for (a_val, b_val), freq no topo: if gcd(b_val, ORDER) != 1: continuar inv_b = pow(b_val, -1, ORDEM) k_candidate = (-a_val * inv_b) % ORDEM top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: quebrar # Verifique o sucesso e imprima os resultados found_k7 = qualquer(k == 7 for (_, k, _) em top_invertibles) Se found_k7: print("\nSUCESSO — k = 7 encontrado nos 100 principais resultados\n") mais: print("\nAVISO — k = 7 NÃO encontrado nos 100 primeiros resultados\n") print("Top 100 pares invertíveis (a, b) e k recuperado:") para (a, b), k, contar em top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (contagem = {contagem}){tag}") # Salvar dados brutos fora = { "experimento": "ECDLP_32pts_Shors", "backend": backend .name, "physical_qubits": FÍSICO, "tiros": TIROS, "conta": counts_raw } JSON_PATH = "/Usuários/steventippeconnic/Documentos/QC/Shors_ECC_5_Bit_Key_0.json" com open(JSON_PATH, "w") como fp: json.dump(saída, fp, recuo=4) log .info("Resultados salvos → %s", JSON_PATH) # Fim Código completo para todas as visualizações usando dados de execução no Qwork.