Bryta en 5-bitars elliptisk kurvnyckel med en kvantdator ⚛️ med 133 kvantbitar Det här experimentet bryter en 5-bitars kryptografisk nyckel med elliptisk kurva med hjälp av Shors algoritm. En krets med 15 kvantbitar, bestående av 10 logiska kvantbitar och 5 ancilla, körs på @IBM:s 133-kvantbits-ibm_torino med @qiskit och interfererar över Z₃₂ för att extrahera den hemliga skalären k från den offentliga nyckelrelationen Q = kP, utan att någonsin koda k direkt in i oraklet. Från 16 384 bilder avslöjar kvantinterferensen en diagonal ås i 32x32 QFT-resultatutrymmet. Kvantkretsen, som var över 67 000 lager djup, producerade giltiga interferensmönster trots extremt kretsdjup, och klassisk efterbehandling avslöjade k = 7 i de 100 bästa inverterbara (a, b) resultaten. Genomgång av kod 1. Kodning av grupper Begränsa uppmärksamheten till undergruppen ordning-32 ⟨P⟩ av en elliptisk kurva över F_p. Mappa punkter till heltal: 0P -> 0, 1P -> 1, ..., 31P -> 31. Grupprätt blir ett modulärt tillägg: (xP) + (yP) = ((x + y) mod 32))P. I detta experiment används en elliptisk kurva över F_p med en cyklisk delgrupp av ordning 32, som avbildar P -> 1 och Q = 7P -> 23 i Z₃₂. Koden förutsätter förberäknad skalär multiplikation och abstraherar bort explicita koordinater. 2. Kvantregister Registrera en: fem kvantbitar för exponenten a ∈ {0, ..., 31}. Registrera b: fem kvantbitar för b ∈ {0, ..., 31}. Registrera p: fem kvantbitar initierade till ∣0⟩ för att lagra punktindexet. Klassiskt register c: ett 10-bitars register för att registrera de uppmätta värdena för a och b. 3. Förberedelse av superposition Tillämpa Hadamards på varje kvantbit i a och b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Konstruktion av orakel U_f Målet är en reversibel karta: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Lägg till aP: för varje bit a_i (vikt 2^i), lägg till (2^i P) mod 32 Lägg till bQ: compute (2^i Q) mod 32, lägg sedan till kontrollerad på b_i. Dessa använder 5-qubit-kontrollerade permutationsgrindar. Alla konstanter härleds från den elliptiska kurvans generator P och den publika punkten Q. Ingen grind refererar någonsin direkt till det hemliga k. 5. Globalt tillstånd efter Oracle Staten utvecklas till: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, där f(a, b) = a + kb (mod32). a, b 6. Isolera punktregister Algoritmen behöver bara fasrelationen i a, b. En barriär isolerar p. 7. Kvant Fourier-transform (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Interferens mönster Den gemensamma amplituden för observation (u, v) är: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), som bildar en diagonal ås i 32x32-utfallsrutnätet. 9. Mätning Mät alla tio logiska kvantbitar. Resultaten koncentrerar sig på de 32 distinkta paren som uppfyller u + kv ≡ 0 (mod 32). 10. Klassisk efterbehandling Bitsträngar är endian-flippade och parsade i (a, b) par. Behåll endast rader där gcd(b, 32) = 1, och se till att b är inverterbart. Kandidatnyckeln beräknas som: k = (-a) b^(-1) mod 32 Skriptet då: Extraherar de 100 främsta inverterbara resultaten (a, b). Beräknar k för varje. Skriver ut varje (a, b) par, återställt k och antal. Deklarerar framgång om k = 7 visas bland de 100 främsta. 11. Verifiering och lagring Den korrekta skalären k = 7 bekräftas om den visas bland de 100 bästa inverterbara resultaten. Alla råa bitsträngar, kvantbitslayout och metadata sparas i JSON för ytterligare visualisering och analys. Resultat 2025-06-25 19:41:29,294 | INFO | Kretsdjup 67428, antal grindar OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Skicka jobb med alternativen {'options': {}, 'version': 2, 'support_qiskit': True} SUCCESS — k = 7 finns bland de 100 bästa resultaten Topp 100 inverterbara par (a, b) och återvunna k: (a = 8, b = 11) → k = 8 (räkning = 63) (a = 12, b = 9) → k = 20 (antal = 58) (a = 0, b = 3) → k = 0 (antal = 54) (a = 1, b = 9) → k = 7 (räkna = 54) <<< (a = 28, b = 1) → k = 4 (räkning = 53) (a = 0, b = 11) → k = 0 (antal = 53) (a = 8, b = 9) → k = 24 (räkning = 53) (a = 8, b = 3) → k = 8 (räkning = 53) ... (a = 11, b = 3) → k = 7 (räkning = 41) <<< ... (a = 25, b = 1) → k = 7 (antal = 32) <<< Denna körning hämtade framgångsrikt den hemliga skalären k = 7 med hjälp av en 5-bitars ECC-nyckel (order-32-undergrupp), vilket utökade min tidigare 4-bitars attack till ett utrymme med 1024 möjliga (a, b) kombinationer och φ(32) = 16 inverterbara b-värden. k = 7 förekommer tre gånger i topp 100: (a = 1, b = 9) -> k = 7 med 54 räkningar (a = 11, b = 3) -> k = 7 med 41 räkningar (a = 25, b = 1) -> k = 7 med 32 räkningar Dessa är högfrekventa tillstånd, vilket gör dem till trovärdiga attackvektorer under klassisk efterbearbetning. Räkningarna uppvisar koncentration kring strukturerade modulära relationer: a + kb ≡ 0 mod 32. Dessa visas som diagonala åsar i mätutrymmet 32x32. Flera k-värden återkommer ofta (k = 0, 24, 28), vilket visar den probabilistiska överlappningen som är inneboende i kvantinterferens, några av dessa är falska positiva från brus eller aliasing med andra modulära ekvivalenser. Kretsdjupet var 67 428, med totalt 106 455 grindar, vilket återspeglar en stor, komplex kvantrutin för kontrollerad modulär indexaritmetik. Detta kan vara den största mängden grindar jag har använt i en krets. Antal grindar för kretsen: Storlek: 56613 CZ: 34319 Rund: 15355 x: 157 Mått: 10 Barriär: 1 Totalt antal grindar: 106455 Djup: 67428 Bredd: 133 kvantbitar | 10 bitar Experimentet tog 54 sekunder att slutföra på "ibm_torino". Brusprofilen är ojämn men sönderfallande, vilket innebär att kvantsystemet sannolikt löste upp dominanta övertoner i interferensen men suddade ut finare strukturer. Distributionssvansen innehåller fortfarande giltiga k = 7 kandidater, detta stöder kvantattacker i ordboksstil där topp-N-resultatgenomsökningar (N = 100) är tillräckliga för att hämta nyckeln. 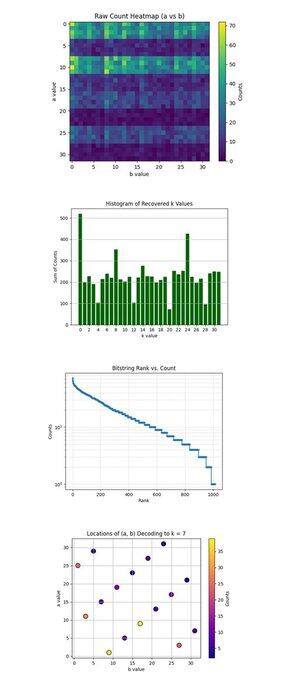Raw Count Heatmap (a vs b) ovan (fullständig kod på Qwork) visar ett 32x32 rutnät som representerar de observerade räkningarna för varje par (a, b) efter att ha kört Shors krets. Värmekartan visar en bandad och ojämn fördelning, vilket indikerar interferenskammar, inte brus. Vissa rader (a-värden) har synbart högre koncentration, vilket tyder på konstruktiv interferens längs specifika a + kb ≡ 0 mod 32-lösningar. Histogrammet över återställda k-värden ovan (fullständig kod på Qwork) aggregerar det totala antalet för varje återvunnen skalär nyckel k ∈ Z₃₂, härledd via k = −ab^(−1) mod 32. En stor topp vid k = 0 och en annan runt k = 24 är dominanta. Den korrekta nyckeln k = 7 är inte den högsta, men är väl representerad (~54 + 41 + 32 = 127 räkningar över flera (a, b) par). Detta visar att hackare kan använda en större mängd resultat. Bitstring Rank vs Count (Log-Scale) ovan (fullständig kod på Qwork) visar ett Zipf-liknande rangdiagram över alla bitsträngar efter fallande antal. Den logaritmiska y-axeln visar en exponentiell svans, de flesta resultat inträffar <10 gånger. Bitsträngarna för huvudet (topp ~50) har brant högre sannolikhet, vilket indikerar konstruktiva interferenstoppar. Du kan skapa en kvantheuristisk ordboksattack som endast skördar de översta N-bitsträngarna med exponentiell retur på signal. Detta validerar att kvantsignal-till-brus-strukturen fortfarande är intakt även med längre kretsar (67428 djup). Platserna för (a, b) avkodning till k = 7 ovan (fullständig kod på Qwork) visar att varje punkt är ett (a, b) par som avkodas till k = 7. Färgintensiteten är lika med antalet gånger som detta par inträffade. Diagrammet visar en relativt jämn fördelning över (a, b), men med lokala toppar vid (1, 9), (11, 3), (25, 1). Multipla (a, b) kombinationer konvergerar till k = 7 med icke-likformig multiplicitet. Ur en kryptoanalytisk synvinkel validerar detta att Shors algoritm på ett tillförlitligt sätt kan knäcka ECC-nycklar även när rätt k inte är topp 1-resultatet. 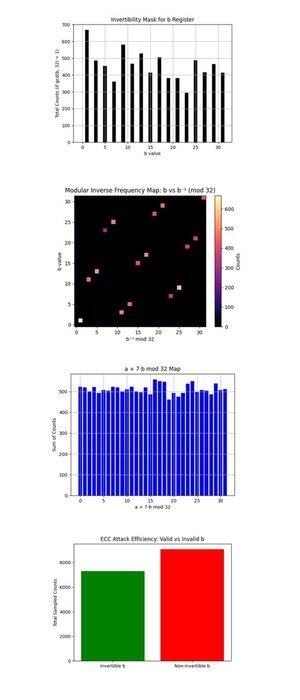Inverterbarhetsmasken för b Register ovan (fullständig kod på Qwork) visar ett stapeldiagram med räkningar för varje b ∈ {0, ..., 31} som är coprime med 32 (gcd(b, 32) = 1, endast dessa är inverterbara modulo 32 och användbara för att återställa k via: k = (−a)b^(−1) mod 32. Inverterbara b är välbefolkade, vilket visar att kretsen faktiskt producerade återvinningsbara kandidater. Mer enhetlighet här skulle öka efterbehandlingskraften, helst skulle dessa vara platta. Modular Inverse Frequency Map: b vs b^(−1) mod 32 ovan (fullständig kod på Qwork) visar en värmekarta över hur ofta varje inverterbar b mappar till varje motsvarande modulär invers b^(−1) mod 32, viktat med resultatantal. De flesta punkter faller på en ren bijektivlinje, varje b avbildas rent till ett unikt b^(−1), vilket bekräftar riktigheten av modulär inversion. Ljusare områden (längst ned till vänster eller längst upp till höger) visar gynnade b från kvantsamplingen. Inget off-diagonalt brus eller klustring, gott tecken på ren modulär struktur bevarad. Kartan a + 7b mod 32 ovan (fullständig kod på Qwork) antar k = 7 och plottar värdet av (a + 7b) mod 32 över alla resultat. Fördelningen är nästan enhetlig. Detta tyder på att det inte finns någon skarp interferenskant som i 4-bitarsfallet. Varför? 5-bitarskretsen (med 10 logiska kvantbitar) sprider amplituden tunnare över 1024-resultat, vilket minskar kontrasten. Ändå gick det fortfarande att återvinna den korrekta nyckeln, vilket indikerade många svagt konstruktiva vägar, snarare än några få dominerande. ECC Attack Efficiency: Valid vs Invalid b ovan (fullständig kod på Qwork) visar totala antal från prover med inverterbar b (användbar för nyckelåterställning) vs. icke-inverterbar b (värdelös). Över hälften av resultaten slösas bort på ogiltiga b-värden (gcd(b, 32) != 1). Nästa design för en 6-bitars brytning kan använda oracle-maskering eller postselection-filtrering på giltiga b-domäner. 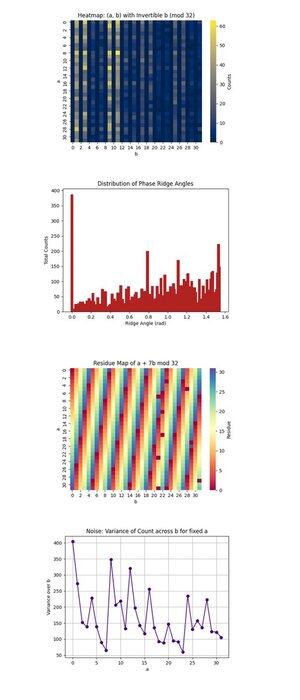Heatmap: (a, b) med Invertible b (mod 32) ovan (fullständig kod på Qwork) fokuserar bara på (a, b) par där b är inverterbar modulo 32, ett nödvändigt villkor för att återställa k. Den visar var kvantinterferensen koncentreras inom utrymmet med 1024 punkter. De högintensiva regionerna avslöjar föredragna interferensvägar, vilket tyder på att kvanttillståndet utvecklades ojämnt, vilket möjligen gynnade vissa banor under modulär multiplikation. Det bekräftar att det finns en tillräckligt stark signal om samstämmighet i vissa regioner för att man ska kunna isolera giltiga kandidater. Fördelningen av fasåsvinklar ovan (fullständig kod på Qwork) placerar vinklarna som bildas av (-a, b) vektorer i planet, modulo π, vilket ungefär motsvarar fasåsar i QFT-rymden. Toppar i histogrammet indikerar starka inriktningar, resonanser, av formen u + kv ≡ 0, vilket innebär att kretsen framgångsrikt kodade k in i interferensmönstret trots att det fulla tillståndsutrymmet är enormt. De många dominanta vinklarna tyder på att övertoner av den dolda förskjutningen är närvarande. Residue Map för a + 7b mod 32 ovan (fullständig kod på Qwork) visualiserar utdataåterstoden för den specifika måltangenten k = 7, över hela (a, b) utrymmet. Eventuella konsistenta band eller symmetrier här indikerar hur väl interferensen förstärkte giltiga lösningar (där detta värde är lika med 0). Du kan observera vilka regioner i 1024-gittret som motsvarar en + 7b ≡ 0, vilket validerar att oraklets struktur ledde till framgångsrik nyckelprägling. Bruset: Variansen av antalet över b för fast a ovan (fullständig kod på Qwork) visar hur bullriga eller stabila utdataräkningarna var för varje fixat a när vi varierar b. Hög varians innebär att vissa b-värden leder till stark förstärkning medan andra inte gör det, vilket innebär kretskänslighet eller backend-brus för den a-raden. Utjämnade regioner innebär kvantkoherens, medan toppar kan peka på dekoherens eller felspridning under orakelutvärderingen. Till slut lyckades det här experimentet knäcka en 5-bitars elliptisk kurvnyckel med hjälp av Shors algoritm som kördes på IBM:s 133-qubit kvantprocessor, vilket utökade det tidigare 4-bitarsresultatet till ett betydligt större interferensutrymme (32x32 = 1024 resultat). Denna krets kodade oraklet över Z₃₂ utan att någonsin referera till den hemliga skalären k, och utnyttjade modulär grupparitmetik för att trassla in skalären i fasinterferens. Kvantkretsen, som var över 67 000 lager djup, producerade giltiga interferensmönster trots extremt kretsdjup, och klassisk efterbehandling avslöjade k = 7 i de 100 bästa inverterbara (a, b) resultaten. Genom visualiseringar bekräftade detta experiment diagonala åsstrukturer, inverterbarhetsmasker och harmonisk inriktning av interferenskammar, vilket validerade att kvantkoherensen förblev tillräckligt stark för att förstärka det korrekta modulära förhållandet. Detta fastställer att Shors algoritm fortsätter att skalas under djupare kretsregimer och att ordboksbaserade nyckelåterställningsstrategier (topp 100-uppräkning) förblir genomförbara när bitlängden ökar, vilket visar tydliga kvantfördelar även under bullriga verkliga förhållanden. Kod # Huvudkrets # Import Importera loggning, JSON Från Math Import GCD Importera numpy som np från qiskit importera QuantumCircuit, QuantumRegister, ClassicalRegister, transpile från qiskit.circuit.library importera UnitaryGate, QFT från qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 Importera Pandas som PD # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANS = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Användare/steventippeconnic/Nedladdningar/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SKOTT = 16384 # Parametrar för leksakskurvan (ordning-32 undergrupp av E(F_p)) ORDNING = 32 # |E(F_p)| = 32 P_IDX = 1 # Generator P -> index 1 Q_IDX = 23 # Offentlig punkt Q = kP, här "23 mod 32" för k = 7 # Hjälp med loggning logging.basicConfig(level=loggar .INFO, format="%(asctime)s | %(nivånamn)s | %(meddelande)s") log = logging.getLogger(__name__) # Kalibreringsbaserat kvantbitsval def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() vinnare = ( df.sort_values(["√x (sx) fel", "T1 (oss)", "T2 (oss)"], ascending=[Sant, Falskt, Falskt]) ["Qubit"].head(n).tolist() ) log .info("Bästa fysiska kvantbitar: %s", vinnare) Returnera vinnare N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, punkt FYSISK = best_qubits(CAL_CSV, N_Q_TOTAL) # Constant-adder modulo 32 som en återanvändbar grind def add_const_mod32_gate(c: int) -> UnitaryGate: """Returnera en grind med 5 kvantbitar som mappar |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) För x inom intervallet(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) för c i intervall(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, konstant): """Använd |x⟩ → |x+konstant (mod 32)⟩ styrs av en kvantbit.""" qc.append(ADDERS[konstant].control(), [ctrl_qubit, *point_reg]) # Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (index aritmetik mod 32) def ecdlp_oracle(QC, a_reg, b_reg, point_reg): För i i intervall(N_Q): konstant = (P_IDX * (1 << i)) % ORDER Om konstant: controlled_add(qc, a_reg[i], point_reg, konstant) För i i intervall(N_Q): konstant = (Q_IDX * (1 << i)) % ORDER om konstant: controlled_add(qc, b_reg[i], point_reg, konstant) # Bygg hela Shor-kretsen def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=Falskt), a) qc.append(QFT(N_Q, do_swaps=Falskt), b) qc.measure(a, c[:N_Q]) qc.mått(b, c[N_Q:]) Returnera qc # Utförande av IBM Runtime tjänst = QiskitRuntimeService(kanal="ibm_cloud", token=TOKEN, instance=INSTANS) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpilera(qc_raw, backend=backend, initial_layout=FYSISKT, optimization_level=3) log .info("Kretsdjup %d, grindantal %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(läge = backend) jobb = provtagare .run([trans], skott=SKOTT) resultat = job.result() # Klassisk efterbehandling creg_name = trans.cregs[0].name counts_raw = resultat[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): returnera int(bs[::-1], 2) antal = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v för k, v i counts_raw.items()} top = sorterad (counts.items(), nyckel = lambda kv: kv [1], reverse = True) # Kriterier för framgång. Kontrollera de 100 översta inverterbara raderna för k = 7 top_invertibles = [] För (a_val, b_val), freq i toppen: if gcd(b_val, ORDNING) != 1: fortsätta inv_b = pow(b_val, -1, ORDNING) k_candidate = (-a_val * inv_b) % ORDER top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: paus # Kontrollera framgång och skriv ut resultat found_k7 = någon (k == 7 för (_, k, _) i top_invertibles) Om found_k7: print("\nSUCCESS — k = 7 hittades i topp 100 resultat\n") annars: print("\nVARNING — k = 7 hittades INTE i topp 100 resultat\n") print ("Topp 100 inverterbara (a, b) par och återvunna k:") För (a, b), k, räkna i top_invertibles: tag = " <<<" om k == 7 annars "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count}){tag}") # Spara rådata ut = { "experiment": "ECDLP_32pts_Shors", "backend": backend .name, "physical_qubits": FYSISK, "skott": SKOTT, "räknar": counts_raw } JSON_PATH = "/Användare/steventippeconnic/Dokument/QC/Shors_ECC_5_Bit_Key_0.json" Med open(JSON_PATH, "w") som fp: json.dump(ut, fp, indrag=4) log .info("Resultat sparade → %s", JSON_PATH) # Slut Fullständig kod för alla visualiseringar som använder kördata på Qwork.