Ruperea unei chei de curbă eliptică pe 5 biți cu un computer ⚛️ cuantic de 133 de qubiți Acest experiment sparge o cheie criptografică cu curbă eliptică de 5 biți folosind algoritmul lui Shor. Executat pe ibm_torino de 133 de qubiți @IBM cu @qiskit, un circuit de 15 qubiți, compus din 10 qubiți logici și 5 ancilla, interferează peste Z₃₂ pentru a extrage scalarul secret k din relația cheie publică Q = kP, fără a codifica vreodată k direct în oracol. Din 16.384 de fotografii, interferența cuantică dezvăluie o creastă diagonală în spațiul de rezultat 32x32 QFT. Circuitul cuantic, cu o adâncime de peste 67.000 de straturi, a produs modele de interferență valide în ciuda adâncimii extreme a circuitului, iar post-procesarea clasică a dezvăluit k = 7 în primele 100 de rezultate invertibile (a, b). Ghid de cod 1. Codificare de grup Restricționați atenția la subgrupul de ordinul 32 ⟨P⟩ al unei curbe eliptice peste F_p. Harta indică numere întregi: 0P -> 0, 1P -> 1, ..., 31P -> 31. Legea grupurilor devine adăugare modulară: (xP) + (yP) = ((x + y) mod 32))P. Acest experiment folosește o curbă eliptică peste F_p cu un subgrup ciclic de ordinul 32, mapând P -> 1 și Q = 7P -> 23 în Z₃₂. Codul presupune înmulțirea scalară precalculată, abstracționând coordonatele explicite. 2. Registre cuantice Registrul a: cinci qubiți pentru exponentul a ∈ {0, ..., 31}. Registrul b: cinci qubiți pentru b ∈ {0, ..., 31}. Registrul p: cinci qubiți inițializați la ∣0⟩ pentru a conține indexul punctual. Registrul clasic c: un registru pe 10 biți pentru a înregistra valorile măsurate ale lui a și b. 3. Pregătirea suprapunerii Aplicați Hadamards la fiecare qubit din a și b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Construcția Oracle U_f Scopul este o hartă reversibilă: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Adăugați aP: pentru fiecare bit a_i (greutate 2^i), adăugați (2^i P) mod 32 Adăugați bQ: compute (2^i Q) mod 32, apoi adăugați controlat pe b_i. Acestea folosesc porți de permutare controlate de 5 qubiți. Toate constantele sunt derivate din generatorul curbei eliptice P și din punctul public Q. Nicio poartă nu face vreodată referire directă la secretul k. 5. Starea globală după Oracle Statul evoluează în: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, unde f(a, b) = a + kb (mod32). a, b 6. Izolați registrul punctelor Algoritmul are nevoie doar de relația de fază în a, b. O barieră izolează p. 7. Transformată Fourier cuantică (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Modelul de interferență Amplitudinea articulară pentru observare (u, v) este: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kV ≡ 0 (mod 32)), care formează o creastă diagonală în grila de rezultate 32x32. 9. Măsurare Măsurați toți cei zece qubiți logici. Rezultatele se concentrează pe cele 32 de perechi distincte care satisfac u + kv ≡ 0 (mod 32). 10. Post-procesare clasică Șirurile de biți sunt inversate și analizate în perechi (a, b). Păstrați numai rândurile în care gcd(b, 32) = 1, asigurându-vă că b este inversabil. Cheia candidată este calculată ca: k = (-a) b^(-1) mod 32 Scenariul atunci: Extrage primele 100 de rezultate invertibile cu cel mai mare număr (a, b). Calculează k pentru fiecare. Imprimă fiecare pereche (a, b), k recuperat și numără. Declară succes dacă k = 7 apare în primii 100. 11. Verificare și depozitare Scalarul corect k = 7 este confirmat dacă apare în primele 100 de rezultate inversabile. Toate numerele brute de șiruri de biți, aspectul qubiților și metadatele sunt salvate în JSON pentru vizualizare și analiză ulterioară. Rezultatele 2025-06-25 19:41:29,294 | INFORMAȚII | Adâncimea circuitului 67428, numărul de porți OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Trimiterea lucrării folosind opțiunile {'options': {}, 'version': 2, 'support_qiskit': True} SUCCES — k = 7 găsit în primele 100 de rezultate Top 100 de perechi inversabile (a, b) și k recuperate: (a = 8, b = 11) → k = 8 (număr = 63) (a=12, b= 9) → k = 20 (număr = 58) (a = 0, b = 3) → k = 0 (număr = 54) (a= 1, b= 9) → k = 7 (număr = 54) <<< (a = 28, b = 1) → k = 4 (număr = 53) (a = 0, b = 11) → k = 0 (număr = 53) (a = 8, b = 9) → k = 24 (număr = 53) (a = 8, b = 3) → k = 8 (număr = 53) ... (a=11, b= 3) → k = 7 (count = 41) <<< ... (a=25, b= 1) → k = 7 (count = 32) <<< Această rulare a recuperat cu succes scalarul secret k = 7 folosind o cheie ECC de 5 biți (subgrup de ordinul 32), extinzând atacul meu anterior pe 4 biți la un spațiu cu 1024 de combinații posibile (a, b) și φ(32) = 16 valori b inversabile. k = 7 apare de trei ori în primele 100: (a = 1, b = 9) -> k = 7 cu 54 de numere (a = 11, b = 3) -> k = 7 cu 41 de numere (a = 25, b = 1) -> k = 7 cu 32 de numere Acestea sunt stări de înaltă frecvență, făcându-le vectori de atac credibili în post-procesare clasică. Numerele prezintă concentrare în jurul relațiilor modulare structurate: a + kb ≡ 0 mod 32. Acestea apar ca creste diagonale în spațiul de măsurare 32x32. Mai multe valori k se repetă adesea (k = 0, 24, 28), arătând suprapunerea probabilistică intrinsecă interferenței cuantice, unele dintre acestea fiind fals pozitive din zgomot sau aliasing cu alte echivalențe modulare. Adâncimea circuitului a fost de 67.428, cu un total de 106.455 de porți, reflectând o rutină cuantică mare și complexă pentru aritmetica indexului modular controlat. Aceasta poate fi cea mai mare cantitate de porți pe care le-am folosit într-un circuit. Porțile contează pentru circuit: Sx: 56613 cz: 34319 RZ: 15355 x: 157 Măsură: 10 Barieră: 1 Total porți: 106455 Adâncime: 67428 Lățime: 133 qubiți | 10 clbiți Acest experiment a durat 54 de secunde pentru a fi finalizat pe "ibm_torino". Profilul de zgomot este neuniform, dar în descompunere, ceea ce înseamnă că sistemul cuantic a rezolvat probabil armonicile dominante în interferență, dar a estompat structurile mai fine. Coada distribuției conține încă k = 7 candidați validi, acest lucru acceptă atacuri cuantice în stil dicționar în care scanările de rezultate din top N (N = 100) sunt suficiente pentru a recupera cheia. 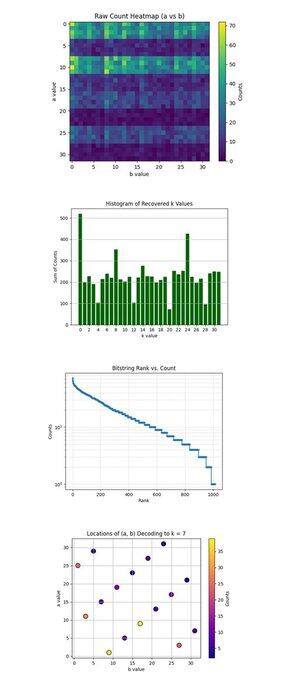Harta termică a numărului brut (a vs b) de mai sus (cod complet pe Qwork) arată că o grilă de 32x32 reprezintă numărul observat pentru fiecare pereche (a, b) după rularea circuitului lui Shor. Harta termică arată o distribuție în benzi și inegală, indicând creste de interferență, nu zgomot. Anumite rânduri (valori a) au o concentrație vizibil mai mare, sugerând interferențe constructive de-a lungul soluțiilor specifice a + kb ≡ 0 mod 32. Histograma valorilor k recuperate de mai sus (cod complet pe Qwork) agregă numărul total pentru fiecare cheie scalară recuperată k ∈ Z₃₂, derivată prin k = −ab^(−1) mod 32. Un vârf uriaș la k = 0 și altul în jurul lui k = 24 sunt dominante. Cheia corectă k = 7 nu este cea mai mare, dar este bine reprezentată (~54 + 41 + 32 = 127 de conturi în mai multe perechi (a, b)). Acest lucru arată că hackerii pot ataca un număr mai mare de rezultate. Bitstring Rank vs Count (Log-Scale) de mai sus (cod complet pe Qwork) arată un grafic de rang asemănător Zipf al tuturor șirurilor de biți prin număr descrescător. Axa y la scară logaritmică arată o coadă exponențială, majoritatea rezultatelor apar de <10 ori. Șirurile de biți head (top ~50) au o probabilitate mult mai mare, indicând vârfuri de interferență constructivă. Ați putea construi un atac de dicționar euristic cuantic care recoltează doar primele N șiruri de biți cu randament exponențial la semnal. Acest lucru validează că structura cuantică semnal-zgomot este încă intactă chiar și cu circuite mai lungi (adâncime 67428). Locațiile (a, b) Decodarea la k = 7 de mai sus (cod complet pe Qwork) arată că fiecare punct este o pereche (a, b) care s-a decodat la k = 7. Intensitatea culorii este egală cu numărul de ori în care a apărut această pereche. Graficul arată o distribuție relativ uniformă între (a, b), dar cu vârfuri locale la (1, 9), (11, 3), (25, 1). Combinații multiple (a, b) converg la k = 7 cu multiplicitate neuniformă. Din punct de vedere criptoanalitic, acest lucru validează faptul că algoritmul lui Shor poate rupe în mod fiabil cheile ECC chiar și atunci când k corect nu este primul rezultat. 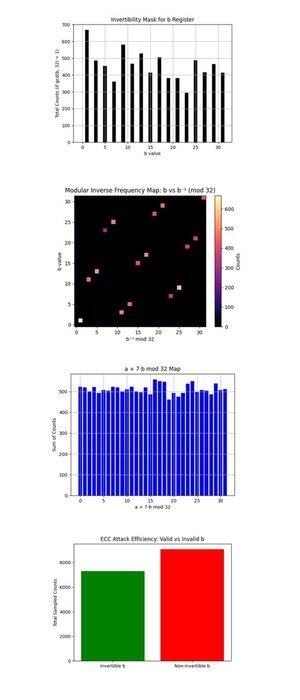Masca de invertibilitate pentru registrul b de mai sus (cod complet pe Qwork) arată o diagramă cu bare a numărătorilor pentru fiecare b ∈ {0, ..., 31} care sunt coprime cu 32 (gcd(b, 32) = 1, numai că acestea sunt invertibile modulo 32 și utile pentru recuperarea k prin: k = (−a)b^(−1) mod 32. B-urile invertibile sunt bine populate, arătând că circuitul a produs candidați recuperabili. Mai multă uniformitate aici ar crește puterea de post-procesare, în mod ideal, acestea ar fi plate. Harta de frecvență inversă modulară: b vs b^(−1) mod 32 de mai sus (cod complet pe Qwork) arată o hartă termică a frecvenței cu cât de des se mapează fiecare b invers modular corespunzător b^(−1) mod 32, ponderat prin numărul de rezultate. Cele mai multe puncte cad pe o linie bijectivă curată, fiecare b se mapează curat la un b^(−1 unic), confirmând corectitudinea inversării modulare. Regiunile mai luminoase (aproape de stânga jos sau dreapta sus) arată b favorizate din eșantionarea cuantică. Fără zgomot sau grupare în afara diagonalei, un semn bun de structură modulară curată păstrată. Harta a + 7b mod 32 de mai sus (cod complet pe Qwork) presupune k = 7 și reprezintă valoarea (a + 7b) mod 32 în toate rezultatele. Distribuția este aproape uniformă. Acest lucru sugerează că nu există o creastă de interferență ascuțită ca în cazul pe 4 biți. De ce? Circuitul pe 5 biți (cu 10 qubiți logici) distribuie amplitudinea mai subțire pe 1024 de rezultate, reducând contrastul. Cu toate acestea, cheia corectă era încă recuperabilă, indicând multe căi slab constructive, mai degrabă decât câteva dominante. Eficiența atacului ECC: Valid vs Invalid b de mai sus (cod complet pe Qwork) arată numărul total de eșantioane cu b inversabil (util pentru recuperarea cheii) vs. b neinversabil (inutil). Peste jumătate din rezultate sunt irosite pe valori b nevalide (gcd(b, 32) != 1). Următorul design pentru o pauză de 6 biți ar putea folosi mascarea oracolului sau filtrarea postselecției pe domenii b valide. 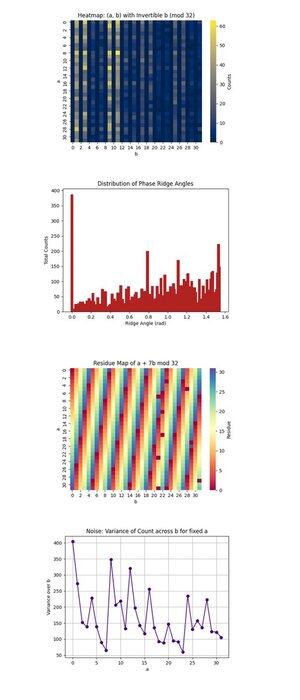Heatmap: (a, b) cu Invertible b (mod 32) mai sus (cod complet pe Qwork) se concentrează doar pe (a, b) perechi unde b este invertibil modulo 32, o condiție necesară pentru recuperarea k. Arată unde se concentrează interferența cuantică în spațiul de 1024 de puncte. Regiunile de mare intensitate dezvăluie căi de interferență preferate, sugerând că starea cuantică a evoluat neuniform, posibil favorizând anumite orbite sub înmulțire modulară. Acesta confirmă o coerență a semnalului suficient de puternică în unele regiuni pentru a izola candidații validi. Distribuția unghiurilor de creastă de fază de mai sus (cod complet pe Qwork) binează unghiurile formate de vectori (-a, b) în plan, modulo π, care corespund aproximativ crestelor de fază în spațiul QFT. Vârfurile din histogramă indică aliniamente puternice, rezonanțe, de forma u + kv ≡ 0, ceea ce înseamnă că circuitul a codificat cu succes k în modelul de interferență, chiar dacă întregul spațiu de stare este vast. Unghiurile dominante multiple sugerează că sunt prezente armonice ale deplasării ascunse. Harta reziduurilor a + 7b mod 32 de mai sus (cod complet pe Qwork) vizualizează reziduul de ieșire pentru cheia țintă specifică k = 7, pe întregul spațiu (a, b). Orice benzi sau simetrii consistente aici indică cât de bine interferența a amplificat soluțiile valide (unde această valoare este egală cu 0). Puteți observa ce regiuni ale rețelei 1024 corespund unui + 7b ≡ 0, validând faptul că structura oracolului a dus la imprimarea cu succes a cheii. Zgomotul: Varianța numărului pe b pentru a fixa a mai sus (cod complet pe Qwork) arată cât de zgomotos sau stabil au fost numărul de ieșiri pentru fiecare a fixat pe măsură ce variem b. Varianța ridicată înseamnă că unele valori b duc la o amplificare puternică, în timp ce altele nu, ceea ce implică sensibilitate a circuitului sau zgomot backend pentru acel rând a. Regiunile netede implică coerență cuantică, în timp ce vârfurile pot indica decoerență sau propagarea erorilor în timpul evaluării oracolului. În cele din urmă, acest experiment a spart cu succes o cheie de curbă eliptică de 5 biți folosind algoritmul lui Shor executat pe procesorul cuantic de 133 de qubiți de la IBM, extinzând rezultatul anterior de 4 biți într-un spațiu de interferență semnificativ mai mare (32x32 = 1024 rezultate). Acest circuit a codificat oracolul peste Z₃₂ fără a face vreodată referire la scalarul secret k și a folosit aritmetica grupurilor modulare pentru a încurca scalarul în interferența de fază. Circuitul cuantic, cu o adâncime de peste 67.000 de straturi, a produs modele de interferență valide în ciuda adâncimii extreme a circuitului, iar post-procesarea clasică a dezvăluit k = 7 în primele 100 de rezultate invertibile (a, b). Prin vizualizări, acest experiment a confirmat structurile de creste diagonale, măștile de invertibilitate și alinierea armonică a crestelor de interferență, validând că coerența cuantică a rămas suficient de puternică pentru a amplifica relația modulară corectă. Acest lucru stabilește că algoritmul lui Shor continuă să se scaleze în regimuri de circuit mai profunde și că strategiile de recuperare a cheilor bazate pe dicționar (top 100 enumerare) rămân viabile pe măsură ce lungimea de biți crește, arătând un avantaj cuantic clar chiar și în condiții zgomotoase din lumea reală. Cod # Circuitul principal # Importuri Înregistrarea în jurnal a importurilor, JSON Din Math Import GCD import numpy ca np din qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpilă de la qiskit.circuit.library import UnitaryGate, QFT din qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 Importați panda ca PD # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANȚĂ = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Utilizatori/steventippeconnic/Descărcări/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" ÎMPUȘCĂTURI = 16384 # Parametrii curbei de jucărie (subgrupul de ordinul 32 al lui E(F_p)) COMANDĂ = 32 # |E(F_p)| = 32 P_IDX = 1 # Generator P -> index 1 Q_IDX = 23 # Punct public Q = kP, aici "23 mod 32" pentru k = 7 # Ajutor de înregistrare logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(nume nivel)s | %(mesaj)s") log = logging.getLogger(__name__) # Alegere qubit bazată pe calibrare def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.coloane = df.columns.str.strip() câștigători = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascendent=[Adevărat, Fals, Fals]) ["Qubit"].head(n).tolist() ) log .info("Cei mai buni qubiți fizici: %s", câștigători) câștigători de retur N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, punct FIZIC = best_qubits(CAL_CSV, N_Q_TOTAL) # Constant-adder modulo 32 ca poartă reutilizabilă def add_const_mod32_gate(c: int) -> UnitaryGate: """Returnează o poartă de 5 qubiți care mapează |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) pentru x în interval(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) pentru c în interval(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constantă): """Aplică |x⟩ → |x+constantă (mod 32)⟩ controlată de un qubit.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (index aritmetic mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): pentru i în interval(N_Q): constantă = (P_IDX * (1 << i)) % ORDINE dacă este constant: controlled_add(qc, a_reg[i], point_reg, constantă) pentru i în interval(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Construiește circuitul Shor complet def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barieră() qc.append(QFT(N_Q, do_swaps=Fals), a) qc.append(QFT(N_Q, do_swaps=Fals), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) Returnare QC # Execuție IBM Runtime service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANȚĂ) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=FIZIC, optimization_level=3) log .info("Adâncimea circuitului %d, numărul porților %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) rezultat = job.result() # Post-procesare clasică creg_name = trans.cregs[0].name counts_raw = rezultat[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v pentru k, v în counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Criterii de succes. Verificați primele 100 de rânduri inversabile pentru k = 7 top_invertibles = [] pentru (a_val, b_val), frecvent în partea de sus: if gcd(b_val, ORDER) != 1: continua inv_b = pow(b_val, -1, ORDINE) k_candidate = (-a_val * inv_b) % COMANDĂ top_invertibles.append(((a_val, b_val), k_candidate, freq)) dacă len(top_invertibles) == 100: sparge # Verificați succesul și imprimați rezultatele found_k7 = any(k == 7 pentru (_, k, _) în top_invertibles) Dacă found_k7: print("\nSUCCES — k = 7 găsit în primele 100 de rezultate\n") altfel: print("\nWARNING — k = 7 NU se găsește în primele 100 de rezultate\n") print("Top 100 perechi inversabile (a, b) și k recuperate:") pentru (a, b), k, contează în top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count}){tag}") # Salvați datele brute afară = { "experiment": "ECDLP_32pts_Shors", "backend": backend .name, "physical_qubits": FIZIC, "shots": SHOTS, "contează": counts_raw } JSON_PATH = "/Utilizatori/steventippeconnic/Documente/QC/Shors_ECC_5_Bit_Key_0.json" cu open(JSON_PATH, "w") ca fp: json.dump(afară, fp, indent=4) log .info("Rezultate salvate → %s", JSON_PATH) # Sfârșit Cod complet pentru toate vizualizările care utilizează date de rulare pe Qwork.