У березні 2023 року Кальча Джонсон і Некія Джексон, двоє старшокласників, довели теорему Піфагора таким чином, який раніше вважався неможливим: за допомогою тригонометрії. Протягом 2000 років з моменту відкриття тригонометрії завжди вважалося, що будь-який передбачуваний доказ теореми Піфагора, заснований на тригонометрії, повинен бути круговим. Фактично, у книзі, що містить найбільшу відому колекцію доказів («Твердження Піфагора» Еліша Луміса), автор стверджує, що «не існує тригонометричних доказів, тому що всі фундаментальні формули тригонометрії самі по собі засновані на істинності теореми Піфагора». Однак це не зовсім точно. Автори висунули новий доказ теореми Піфагора, який ґрунтується на фундаментальному результаті тригонометрії — законі синусів — і вони демонструють, що доказ не залежить від піфагорійської тотожності sin²x + cos²x = 1.

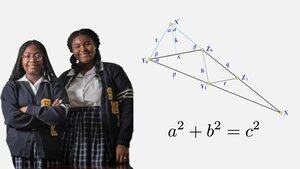
С-К. Шейн, аналіз доказів Кальчі Джонсон і Не'Кії Джексон є чудовою статтею для вашого літнього списку 📚 літератури: