W marcu 2023 roku Calcea Johnson i Ne'Kiya Jackson, dwie uczennice szkoły średniej, udowodniły twierdzenie Pitagorasa w sposób, który wcześniej uważano za niemożliwy: używając trygonometrii. W ciągu 2000 lat od odkrycia trygonometrii zawsze zakładano, że jakiekolwiek rzekome dowody twierdzenia Pitagorasa oparte na trygonometrii muszą być okrężne. W rzeczywistości, w książce zawierającej największą znaną kolekcję dowodów (Twierdzenie Pitagorasa autorstwa Elishy Loomisa), autor stwierdza, że "Nie ma dowodów trygonometrycznych, ponieważ wszystkie podstawowe wzory trygonometrii opierają się na prawdzie twierdzenia Pitagorasa." Jednak to nie jest całkowicie dokładne. Autorzy opracowali nowy dowód twierdzenia Pitagorasa, który opiera się na fundamentalnym wyniku w trygonometrii — prawie sinusów — i wykazują, że dowód jest niezależny od tożsamości Pitagorasa sin²x + cos²x = 1.

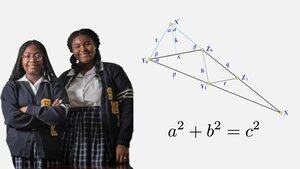
Analiza C-K Shene dotycząca Calcei Johnson i Ne'Kiyi Jackson to świetny artykuł na twoją letnią listę lektur 📚 :